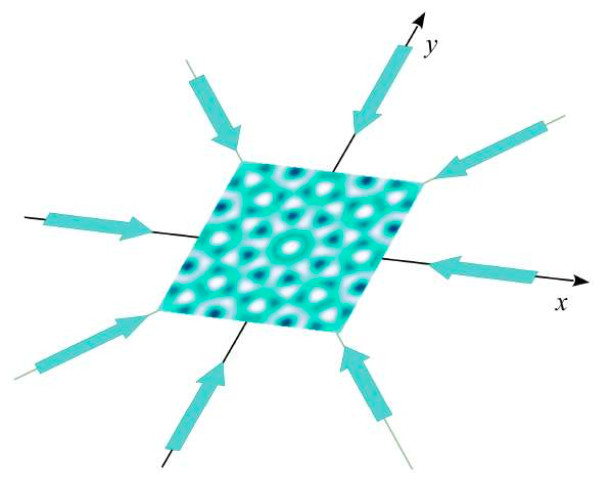
Abstract (click on text): Long-range interacting quantum systems have attracted considerable attention in recent years both from an experimental and theoretical perspective. The class of long-range systems considers the all-to-all interaction of any two constituents whereas the interaction strength falls off algebraically with distance. Latest experimental and technological progress made it possible to realise long-ranged systems on several quantum simulation platforms, including artificial ion crystals and dipolar quantum gases. In the theoretical framework of quantum many-body systems, long-range interactions break various fundamental concepts and theorems with far-reaching consequences. Among those are Lieb-Robinson bounds which guarantee the emergence of causality in short-ranged non-relativistic lattice systems. In this thesis, we study the effects of long-range interactions on out-of-equilibrium and in-equilibrium features of lattice spin models by employing complementary analytical calculations and state-of-the-art tensor-network simulations while particularly focusing on the central and unique quantum feature of entanglement. First, in the long-range transverse-field Ising model, we show the emergence of a weak form of causality characterised by non-universal dynamical exponents. On the one hand, local magnetisation and correlations have an emergent sub-ballistic causal cone while the marked features in the interior of it propagate super-ballistic or ballistic, respectively. On the other hand, the emergent causal cone for all entanglement entropies is shown to be ballistic irrespective of the interaction range and the interior is without marked features. Second, we determine the equilibrium quantum phase diagram of the long-range XXZ model in terms of the anisotropic coupling and the long-range interaction exponent through studying a representation of the spectrum of the reduced density matrix following a half-chain bipartition, the so-called entanglement spectrum. We show it exhibits a remarkable self-similarity within the critical phase where the system is described by a Luttinger liquid while the self-similarity extends to the geometric entanglement and the Luttinger parameter. The transition away from a Luttinger liquid is consistent with the breakdown of self-similarity and a renormalisation group analysis. The synergetic combination of the two latter allows us to locate the corresponding phase transitions which we corroborate by numerical simulations. Furthermore, we show the entanglement Hamiltonian, the Hermitian operator whose spectrum is the entanglement spectrum, follows the form of the Bisognano-Wichmann theorem in large regions of the phases which include the short-range limit, while such a form can be excluded in the phase where genuinely long-ranged effects are relevant. Our results shed new light through the lens of quantum entanglement on the out-of-equilibrium as well as ground state features of long-range interacting spin chains and pave the way for further experimental and theoretical studies.

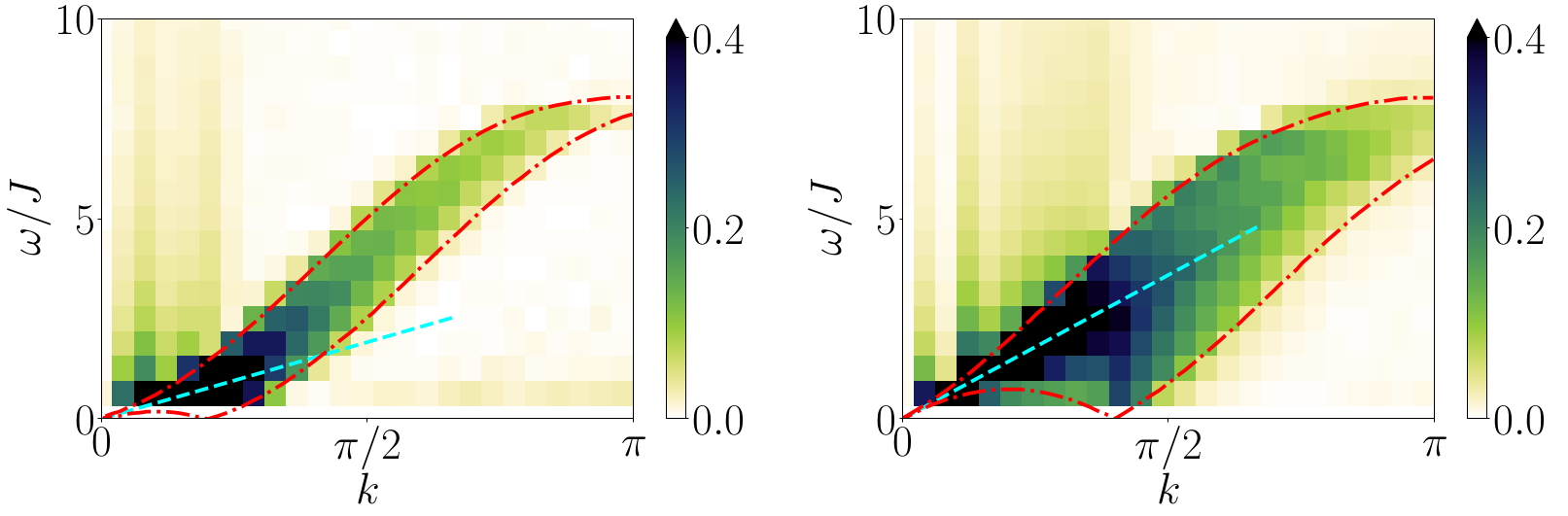
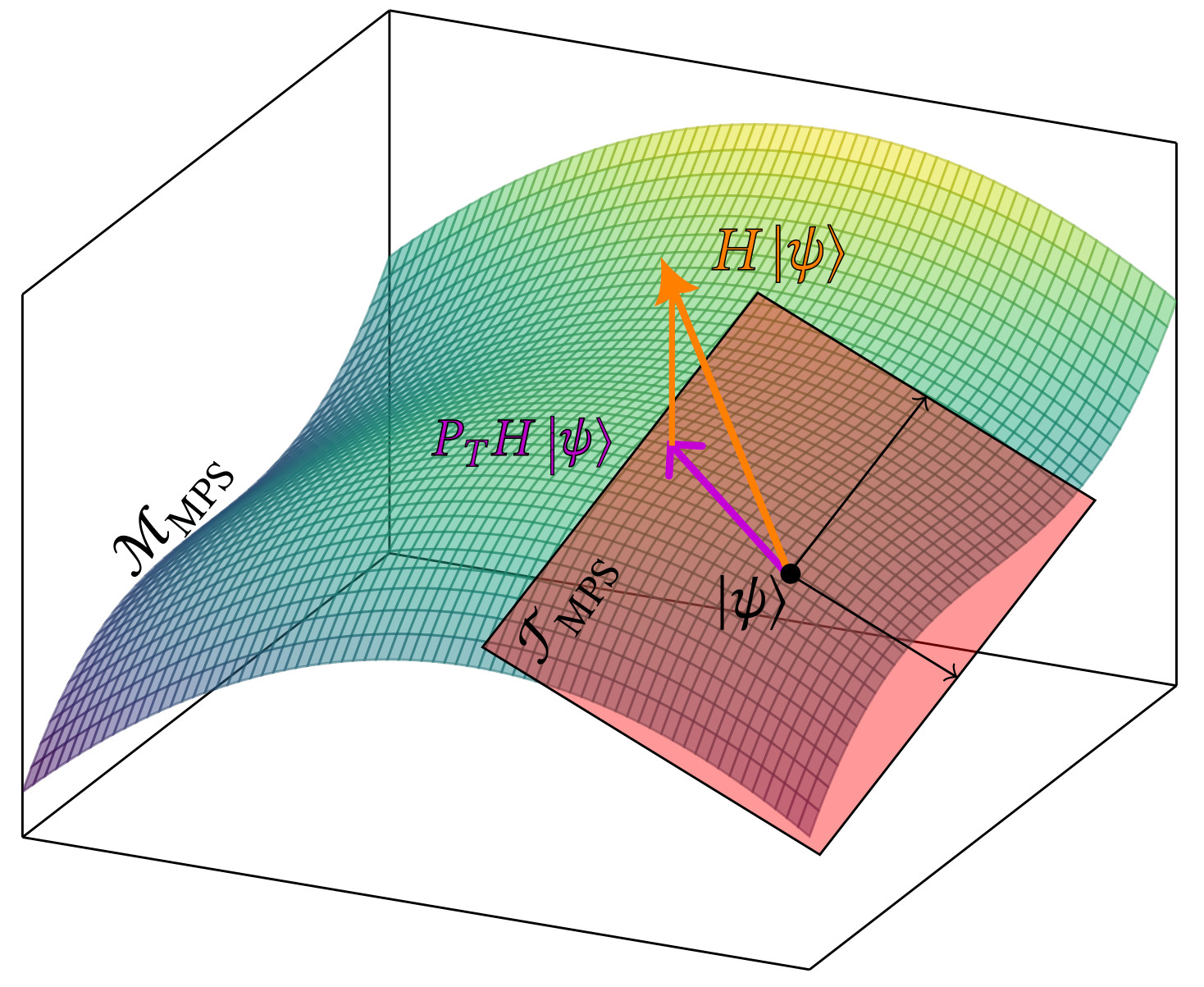
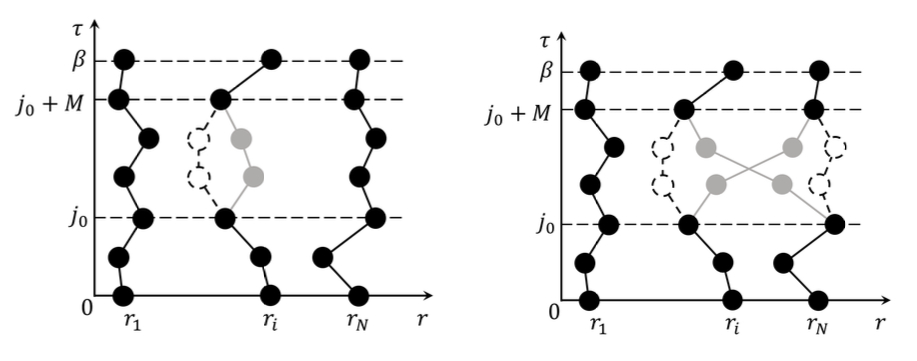
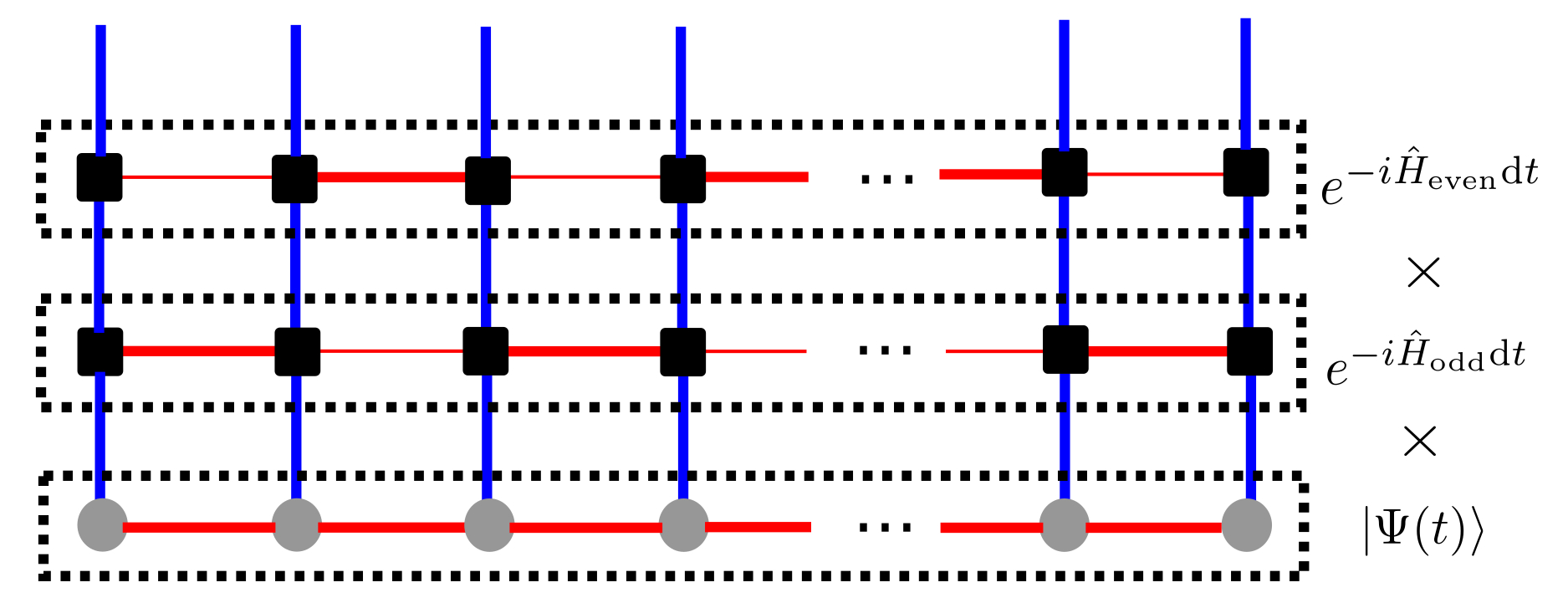
Abstract (click on text): Ultracold atoms have emerged as a versatile platform to realise and control strongly-correlated quantum systems. Spectroscopic methods are the common tools to probe the properties of the excitations which control dynamical transport phenomena. In this thesis, we develop a novel spectroscopic method named quench spectroscopy that uses the out-of-equilibrium dynamics generated by a quantum quench to grant momentum-resolved information about the excitations. We benchmark the method on one-dimensional models where efficient density matrix renormalisation group numerical simulations are available. First, we analyse the out-of-equilibrium space-time pattern of quantum correlations in lattice models following a quantum quench. It displays a generic light-cone like pattern with a twofold structure. Two characteristic velocities can be extracted from the correlations close to the cone edge, one of which gives the velocity for the propagation of quantum correlations throughout the system. Both of these velocities can be related to dynamical properties of the excitation spectrum of the underlying model. Second, we discuss how quench spectroscopy reconstructs spectral properties from space-time patterns using simple equal-time observables or correlators. It allows to reconstruct the full dispersion relation from a series of snapshots of the experiment using quantum gas microscopes, and avoids the tedious scan and calibration in momentum necessary in standard pump-probe methods. We investigate both global and local quenches on clean systems, and discuss the role played by the observable on the spectral features. We discuss the implementation on various examples including the Bose-Hubbard model and spin chain models in various phases, regimes and for different observables. Third, we extend quench spectroscopy to disordered systems. Using as an example the disordered Bose-Hubbard chain, we show using a single probe how the method can unambiguously tell apart the Bose glass from the Mott insulator and the superfluid. Using a spatially-resolved spectral probe, we also reconstruct the full phase diagram of the model.

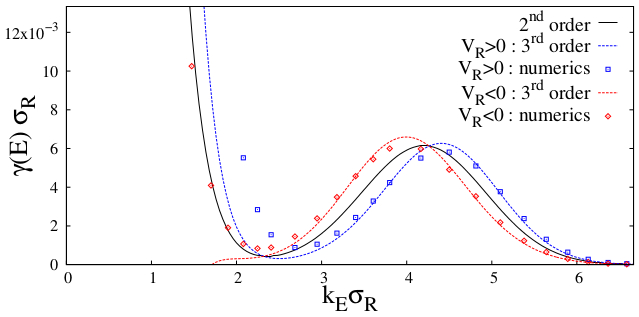
Abstract (click on text): In this thesis, we investigate the properties of one-dimensional bosons in various types of systems, focusing on the phase transitions or crossovers between different quantum degeneracy regimes. Combining quantum Monte Carlo with other standard techniques such as exact diagonalization and thermal Bethe ansatz, we can compute the behavior of 1D bosons in different cases where the results are still lacking. Firstly, in the case of harmonically trapped continuous bosons, we provide a full characterization of a quantity called Tan's contact. By computing the universal scaling function of it, we identify the behavior of the contact in various regimes of degeneracy for 1D bosons. We show that the contact exhibits a maximum versus temperature and that it is a signature of the crossover to fermionization in the strongly-interacting regime. Secondly, we study the localization and fractal properties of 1D ideal gases in shallow quasiperiodic potentials. The quasiperiodic system provides an appealing intermediate between long-range ordered and genuine disordered systems with unusual critical properties. While the tight-binding Aubry-Andre (AA) model has been widely studied, the shallow lattice case behaves differently. We determine the critical localization properties of the system, the critical potential, mobility edges and critical exponents which are universal. Moreover, we calculate the fractal dimension of the energy spectrum and find it is nonuniversal but always smaller than unity, which shows the spectrum is nowhere dense. Finally, we move to the study of the interacting case. With the quantum Monte Carlo calculations, we compute the phase diagram of Lieb-Liniger bosons in shallow quasiperiodic potentials. A Bose glass, surrounded by superfluid and Mott phases, is found. At finite temperature, we show that the melting of the Mott lobes is characteristic of a fractal structure and find that the Bose glass is robust against thermal fluctuations up to temperatures accessible in experiments.

Abstract (click on text): In this thesis, we have investigated the spreading of quantum correlations in isolated lattice models with short- or long-range interactions driven far from equilibrium via sudden global quenches. A main motivation for this research topic was to shed new light on the conflicting results in the literature concerning the scaling law of the correlation edge, its lack of universality and the incompleteness of the existing physical pictures to fully characterize the propagation of quantum correlations. To do so, we have presented a general theoretical approach relying on a quasi-particle theory. The latter has permitted to unveil a generic expression for the equal-time connected correlation functions valid both for short-range and long-range interacting particle and spin lattice models on a hypercubic lattice. Relying on stationary phase arguments, we have shown that its causality cone displays a universal twofold structure consisting of a correlation edge and a series of local extrema defining the outer and inner structures of the space-time correlations. For short-range interactions, the motion of each structure is ballistic and the associated spreading velocities are related to the group and phase velocites of the quasi-particle dispersion relation of the post-quench Hamiltonian. For long-range interactions,the correlation spreading is substantially different due to a possible divergence of group velocity when tuning the interaction range. For a divergent group velocity, ie. the quasi-local regime, we have presented evidence of a universal algebraic structure for the causality cone. While, the correlation edge motion has been found to be always slower than ballistic, the local extrema propagate faster than ballistically and ballistically for gapless and gapped quantum systems respectively. For the local regime implying a well-defined group velocity, we have recovered similar scaling laws and spreading velocities than the short-range case for the causality cone of correlations. The previous theoretical predictions have been verified numerically using tensor network techniques within the case study of the short-range Bose-Hubbard chain and the long-range S= 1/2 XY and transverse Ising chains.

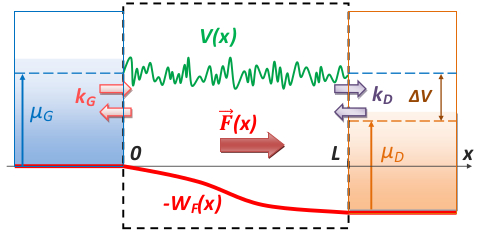
Abstract (click on text): Dans un milieu désordonné, une onde peut être localisée exponentiellement par des effets d'interférence. Ce phénomène de localisation d'Anderson conduit notamment à une annulation de la conductance d'un fluide quantique unidimensionnel. Des travaux théoriques ont cependant montré que l'application d'un champ électrique pouvait réduire, voire supprimer, cette localisation. Nous étudions ici l'effet d'une force sur la localisation d'une onde quantique de matière dans un système unidimensionnel. En lien direct avec les expériences d'atomes ultrafroids, qui permettent d'observer la localisation d'Anderson d'un paquet d'onde en étalement, ou bien l'effet du désordre sur le transport entre deux réservoirs, nous nous intéressons à deux systèmes : la diffusion et la transmission d'une particule. Afin d'étudier la transmission à travers un guide, nous étendons un formalisme de matrices de transfert à la présence d'une force, éventuellement inhomogène. Deux approches analytiques complémentaires nous permettent d'étendre les résultats au cas d'un désordre de tavelures tel que celui utilisé dans les expériences d'atomes ultrafroids. Nous montrons que la force peut être entièrement prise en compte à l'aide d'une renormalisation de la longueur du guide par un libre parcours moyen local de la particule. Pour un désordre blanc, la force conduit alors une localisation plus faible, algébrique, tandis qu'une délocalisation apparaît pour un désordre corrélé. Nous nous intéressons ensuite à la diffusion d'une particule, à l'aide d'une approche numérique. Nous mettons en évidence une délocalisation de la position à grande force sous la forme d'une croissance temporelle algébrique, dont l'exposant augmente avec la force. Nous montrons de plus que la localisation est systématiquement détruite dans un désordre corrélé.

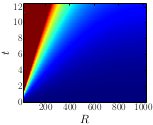
Abstract (click on text): In this thesis we present our results on the propagation of correlations in long-range interacting quantum systems. The dynamics of local observables in these systems cannot be described with the standard methods used in equilibrium statistical physics and completely new methods have to be developed. Several bounds on the time evolution of correlations have been derived for these systems. However the propagation found in experimental and numerical results is completely different and several regimes are present depending on the long-range character of the interactions. Here we present analytical expressions to describe the time evolution of generic observables in systems where the Hamiltonian takes a quadratic form with long- and short-range interactions. These expressions describe the spreading of local observables as the spreading of the fundamental excitations of the system. We apply these expressions to a spin model finding three different propagation regimes. They can be described qualitatively et quantitatively by the divergences in the energy spectrum. The most important result is that the propagation is at most ballistic, but it can be also significantly slower, where the general bounds predict a propagation faster than ballistic. This points out that the bounds are not able to describe properly the propagation, but a more specific approach is needed. We then move to a system of lattice bosons interacting via long-range interactions. In this case we study two different observables finding completely different results for the same interactions: the spreading of two-body correlations is always ballistic while the one of the one-body correlations ranges from faster-than-ballistic to ballistic. Using our general analytic expressions we find that different parts of the spectrum contribute differently to different observables determining the previous differences. This points out that an observable-dependent notion of locality, missing in the general bounds, have to be developed to correctly describe the time evolution.

Abstract (click on text): In this thesis, we theoretically investigate the collective localization properties of weakly-Interacting Bose superfluids subjected to disordered or quasiperiodic potentials. While disorder has been recognized since Anderson to induce single-Particle localization, the interplay between disorder and interactions in quantum systems is today among the most challenging questions in the field, and underlies fascinating phase transitions and non-Trivial localization effetcs. Focusing on Bose gases in the weakly-Interacting regime for which the Bogoliubov theory proves a successful tool, we study the localization transitions of collective excitations in several contexts. First, in the case of a continuous true disorder, we develop a strong-Disorder formalism going beyond previous studies, providing us with a complete description of the localization behaviour of collective excitations in arbitrary dimension. A generic localization diagram is obtained and the transport of excitations in the disorder is microscopically interpreted. Secondly, we consider the case of one-Dimensional quasiperiodic potentials, which are known to display intermediate properties between periodic and disordered ones. We perform a numerical and analytical treatment of the localization problem of collective excitations, allowing us to quantitatively characterize and interpret the localization transition in terms of an effective multiharmonic problem. Finally, we set up the general inhomogeneous formalism to address such issues in multicomponent Bose gases, and enlighten the basic physic of such systems, which are known to exhibit their own specific features.

Abstract (click on text): In this thesis we investigate quantum transport and Anderson localization of non- interacting matterwaves in anisotropic disorder. Using microscopic approaches, we study the effect of disorder correlations, which are shown to significantly modify quantum transport properties in 1D, 2D and 3D. We develop general theoretical tools and apply them to particular models of continuous disorder, which are relevant to ultracold atom experiments : speckle potentials. First, in the one-dimensional case we extend previous models for the localization process of ultracold atoms expanding in a standard speckle potential and show that taking into account new ingredients could permit to understand deviations between experiments and theory observed previously. We then study quantum transport and Anderson localization in dimensions higher than one, with special emphasis on anisotropic correlations, which are naturally present in most speckle potentials. We compute quantum transport properties and propose a new method to estimate the 3D localization threshold (mobility edge). Our theoretical findings are compared with the results of two recent experiments which report evidence of 3D localization of matterwaves. Eventually, we further study effects of disorder correlations, which can induce inversion of localization anisotropies and enhancement of Anderson localization with the particle energy, when appropriately tailored.

Abstract (click on text): Disorder plays a fundamental role in many fields of physics such as condensed-matter physics, optics, acoustics, or atomic physics. It is responsible for a number of surprizing effects, such as Anderson localization, metal-insulator transitions and intriguing glass phases. The inherent complexity of disordered systems poses outstanding challenges to the full understanding of these phenomena. In the last years, disorder has emerged as a major line of research in the field of ultracold quantum gases. The latter offer fascinating perspectives to better understand the effects of disorder in quantum systems, thanks not only to an unprecedented control of parameters, but also to their original properties. This Habilitation thesis reviews our recent contributions to the theory of disordered quantum gases along three main lines: - Anderson localization in disordered quantum gases; - Disorder in interacting Bose gases; - Simulating extended Hubbard and spin models with ultracold gases. On the one hand, we propose and analyze experiments aiming at realizing quantum simulators to address open questions of fundamental importance for the field of disordered systems. In this respect, we show that quantum gases offer promising perspectives. On the other hand, we lead prospective works, which in particular show that quantum gases have original properties. They hence shed new light on issues of broad interest in the field of disordered systems.

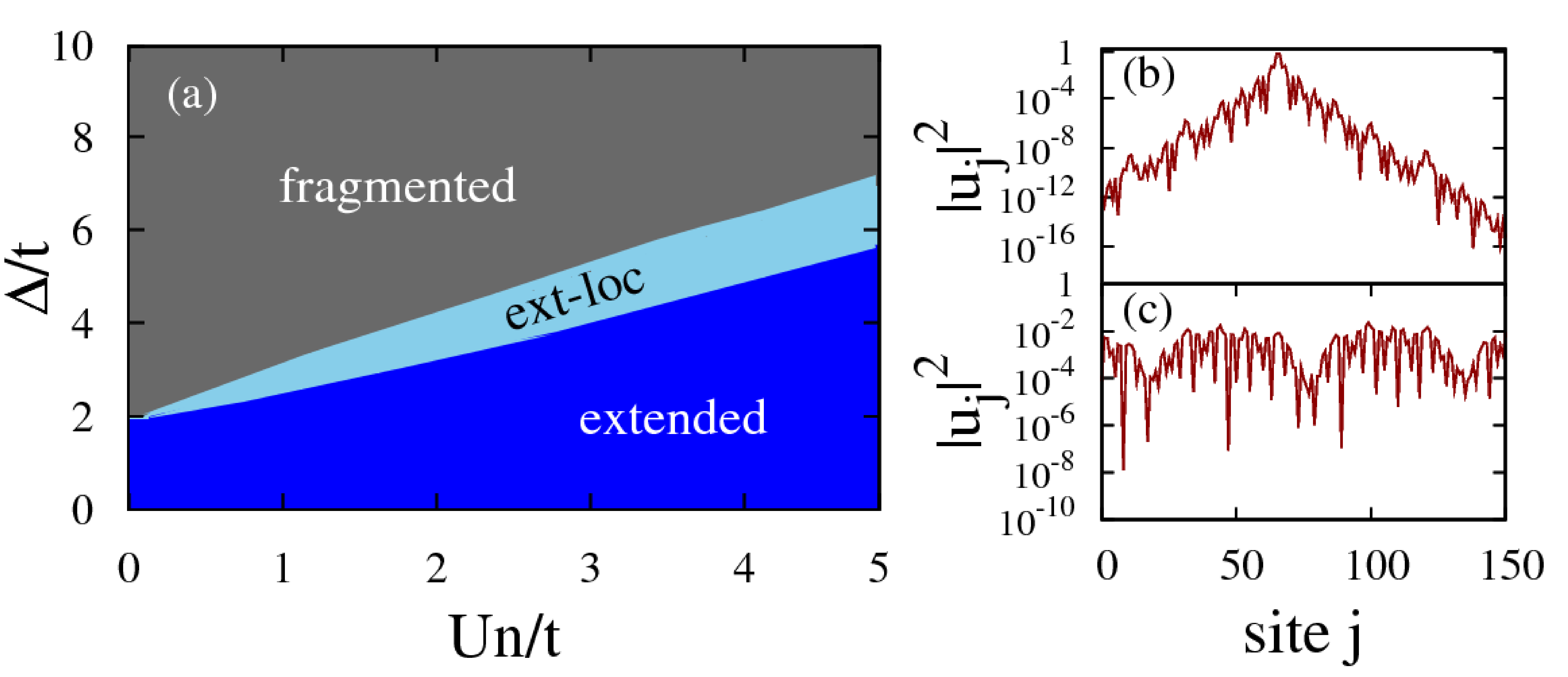
Abstract (click on text): In this thesis, we theoretically investigate the localization properties of weakly-interacting Bose gases in the presence of one-dimensional disorder. We focus on three aspects of those disordered systems. First, we study the case of a non-interacting gas. According to general results, all single-particle states are localized in one dimension. We show that for certain classes of correlated disorder, the dependence of the localization length of the atoms on their energy undergoes sharp crossovers for weak disorder. These findings allow for the interpretation of recent experiments beyond previous analyses. Then, we examine the ground state of an interacting gas, and establish a diagram of the quantum states as a function of the strength of disorder and interactions. We analyze the density modulations imposed on the gas by the disorder, in order to describe the crossover from the regime of delocalized Bose-Einstein condensate to the regime of fragmented condensate. For the regime of very weak interactions, we develop a microscopic description of the system on the basis of the eigenstates of the single-particle Hamiltonian. These results contribute to characterizing the Bose-glass phase at weak interactions, which has yet to be explored thoroughly. Finally, we study the localization of the elementary excitations of the Bose gas in the (quasi-) condensate regime. We show that the suppressed localization of the excitations of lowest energy is due to an efficient screening by the (quasi-) condensate of the long-wavelength variations of the external potential.