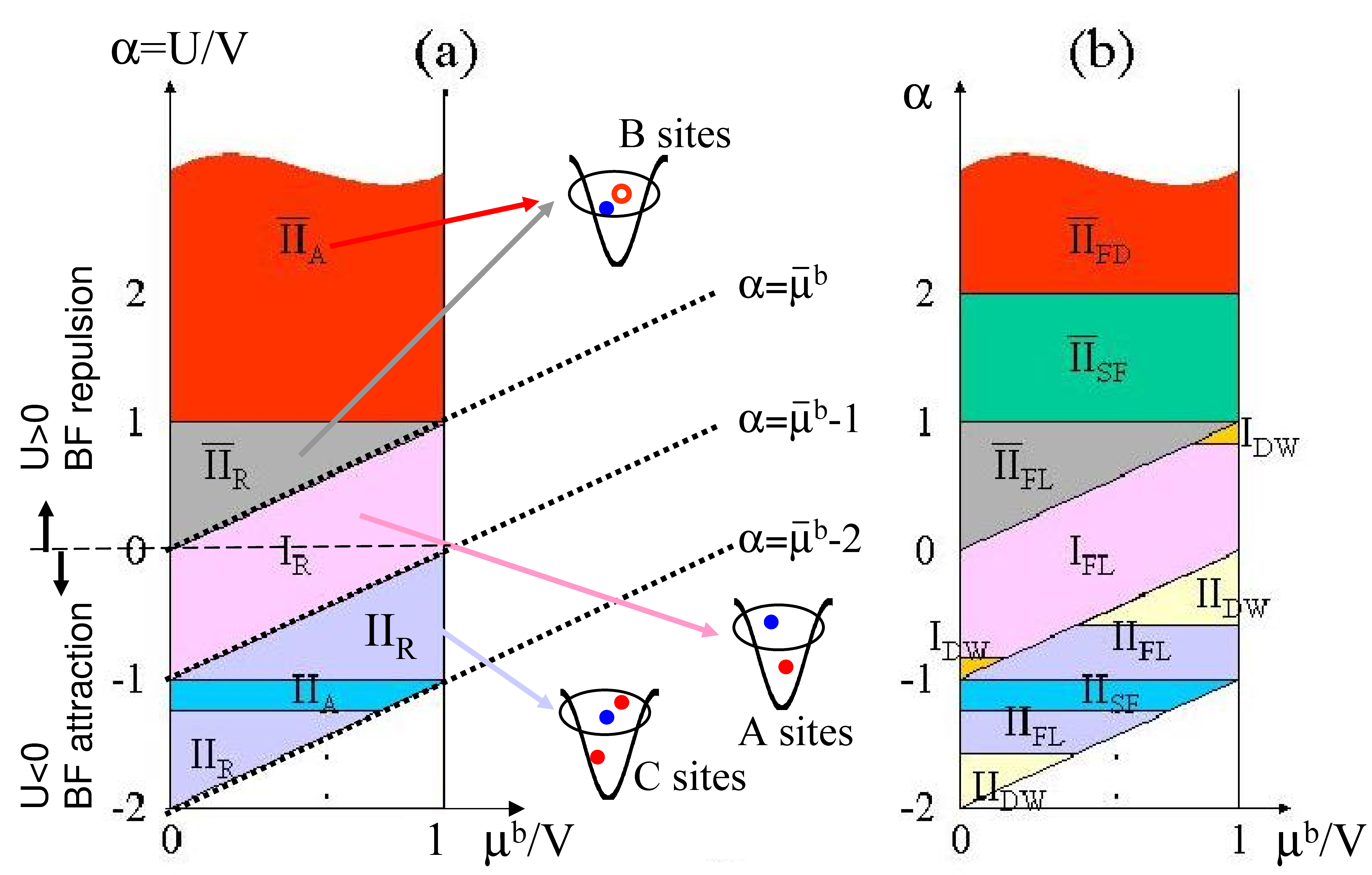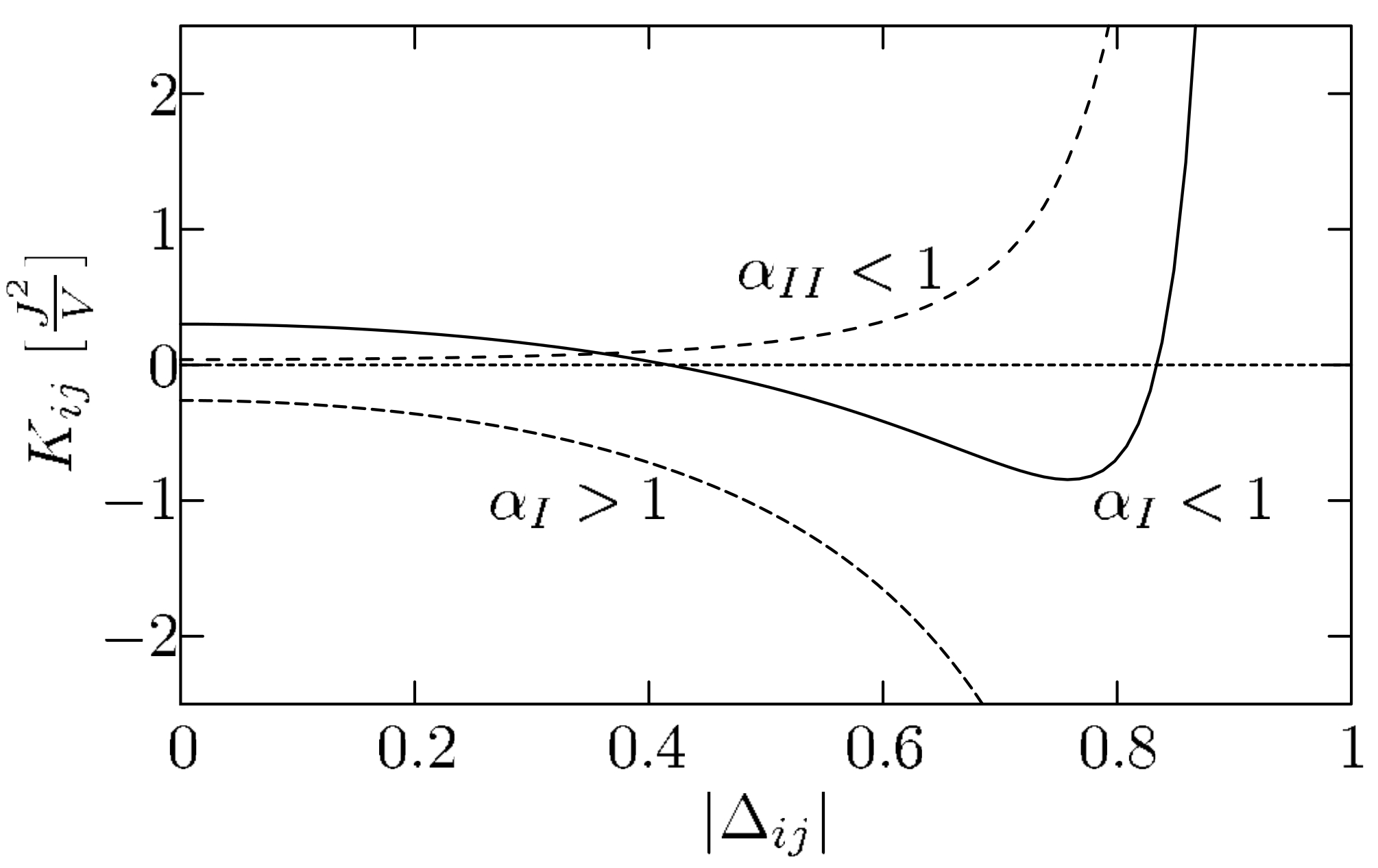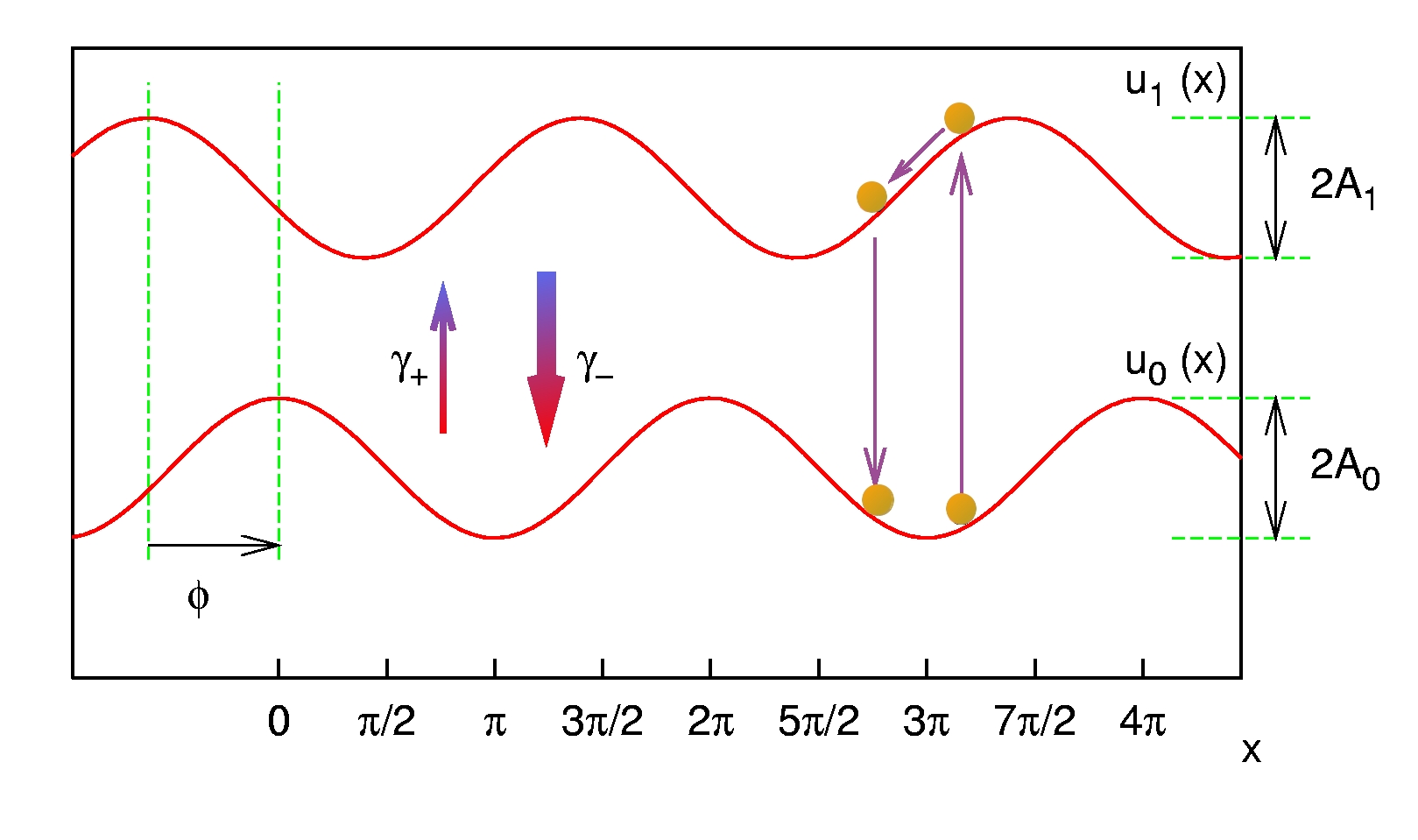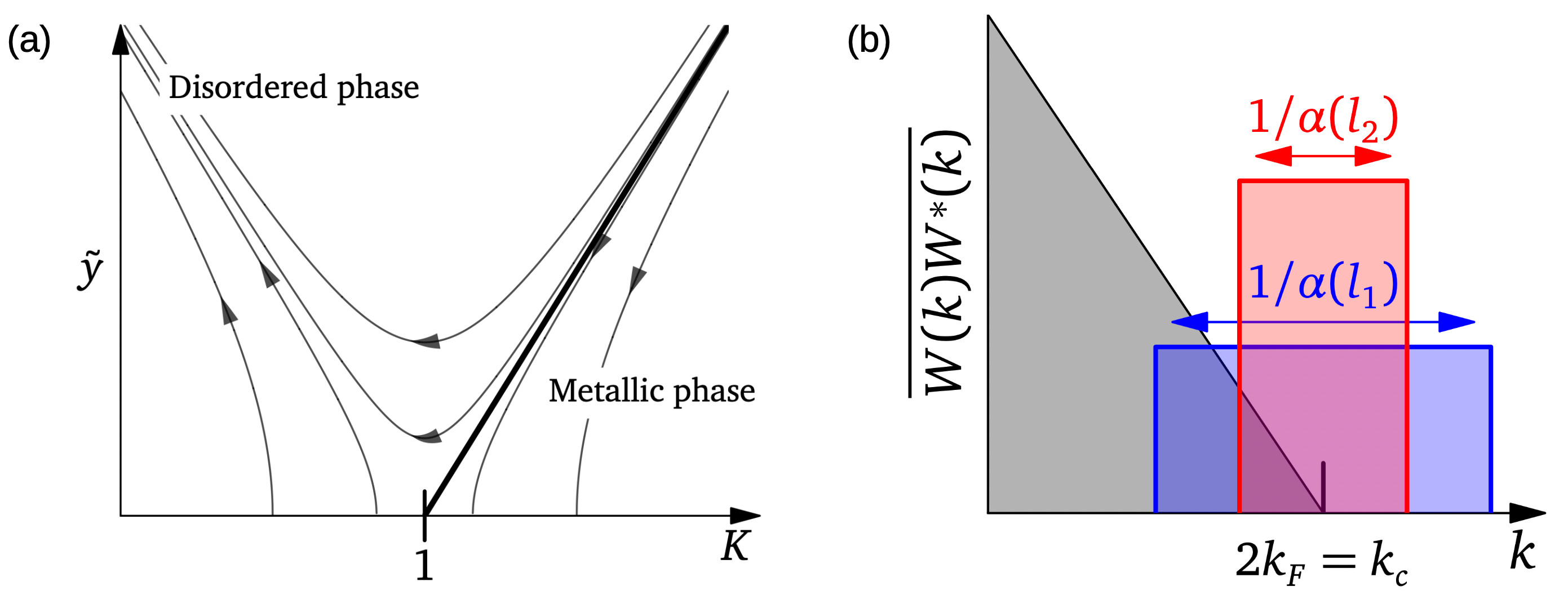
Abstract: We investigate the localization transition of interacting particles in a one-dimensional correlated disorder system. The disorder which we investigate allows for vanishing backwards scattering processes. We derive by two renormalization group procedures its phase diagram and predict that the localization transition point is shifted from finite attractive interaction to the non-interacting point. We finally show numerically that the scaling of the localization length with the disorder strength deviates from the usual scaling of a localized phase.
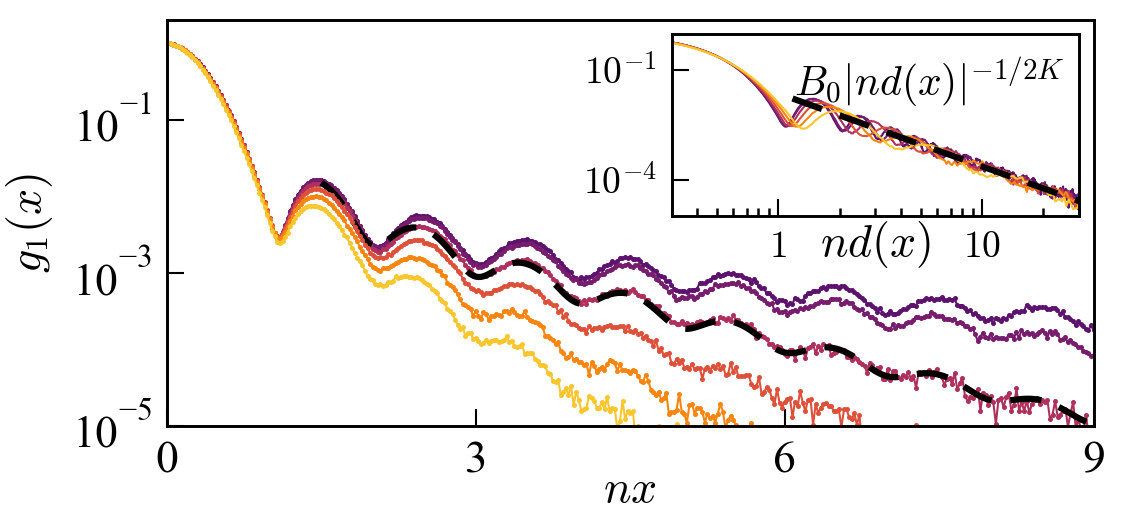
Abstract: The quantum hard rod model, a one-dimensional extension of the Lieb-Liniger model, is exactly solved using an adapted Bethe ansatz. Our solution, benchmarked against path-integral quantum Monte Carlo calculations, reveals significant corrections to the excitation spectrum and thermodynamic properties, previously overlooked by the standard excluded-volume approach. We also show that the hard rod model exhibits Luttinger liquid behavior across a wide range of parameters, at zero and finite temperature, as unveiled by correlation functions. This work provides a comprehensive framework for understanding strongly correlated regimes in dilute 1D systems, with applications to quantum wires, spin chains, and ultracold atoms.
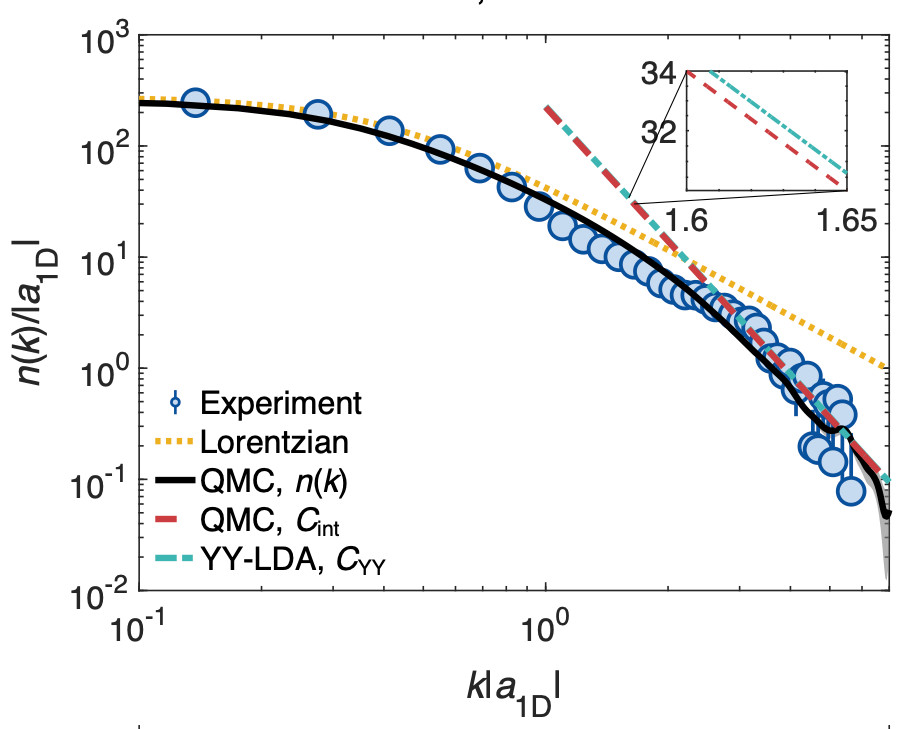
Abstract: The Tan contact has emerged as a pivotal quantity in characterizing many-body quantum systems, bridging microscopic short-range correlations to thermodynamic behavior. It is defined as the weight of universal $1/k^4$ fall off in momentum distribution tails, which can be measured directly in ultracold gases. So far, however, its direct measurement has been hindered in Bose gases due to interactions strongly affecting the expansion dynamics. Here, we present the first direct measurement of the Tan contact in a strongly-correlated Lieb-Liniger gas. Leveraging the one-dimensional geometry of our system, we implement a two-stage expansion scheme, yielding interaction-immune time-of-flight imaging. Our results show excellent agreement with theoretical predictions from quantum Monte Carlo calculations, which also provides independent thermometry of the experiment. By varying atom number, temperature, and interaction strength, we obtain results consistent with the universal scaling law predicted for the trapped Lieb-Liniger model. Our work paves the way for further characterization of the Lieb-Liniger gas across broad interaction regimes and holds promise for extension to other correlated quantum gases in confined geometries.
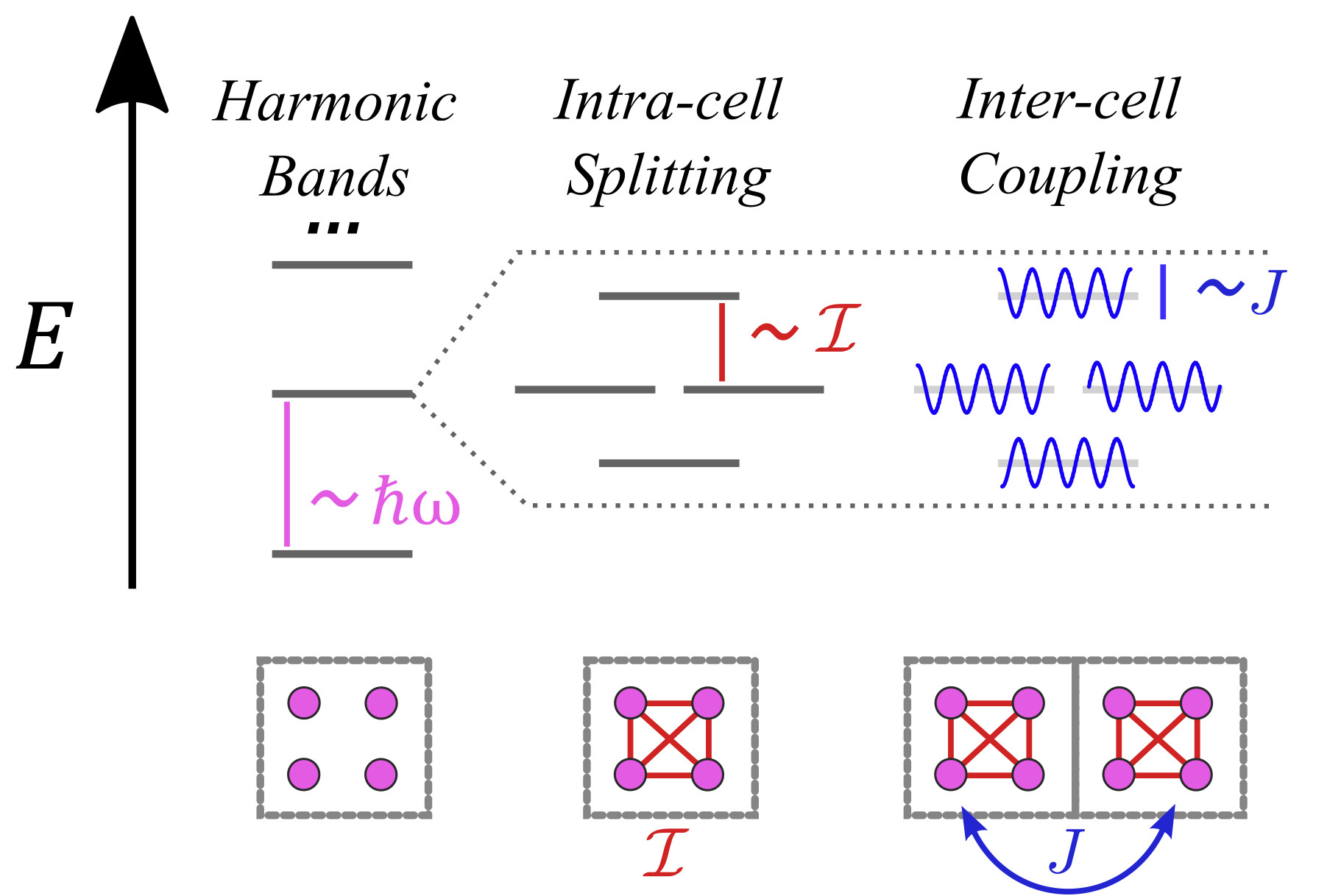
Abstract: A twist between two periodic systems offers the possibility to drastically control quantum transport properties. At discrete sets of commensurate twisting angles, a moiré periodic pattern is formed, and the low-energy single-particle spectrum forms distinct bands and gaps. Here, we consider twisted systems at a commensurate angle made of two continuous-space periodic potentials. We devise a general approach, based on a hierarchy of energy scales, to derive effective tight-binding models that capture the energy spectrum, focusing on the case of square lattices. Localized states in the moiré unit cell are coupled by strong intracell and weak intercell tunnelings, generating a series of energy bands and subbands that correspond to distinct, periodic lattices. For sufficiently deep potentials, we find excellent agreement between the spectrum of the continuous-space system and the tight-binding approximation thus constructed. Our approach allows for the interpretation of moiré band structures and the extraction of parameters for the effective tight-binding models. Applications to the physics of many-body systems and extensions to other twisted models are also discussed.
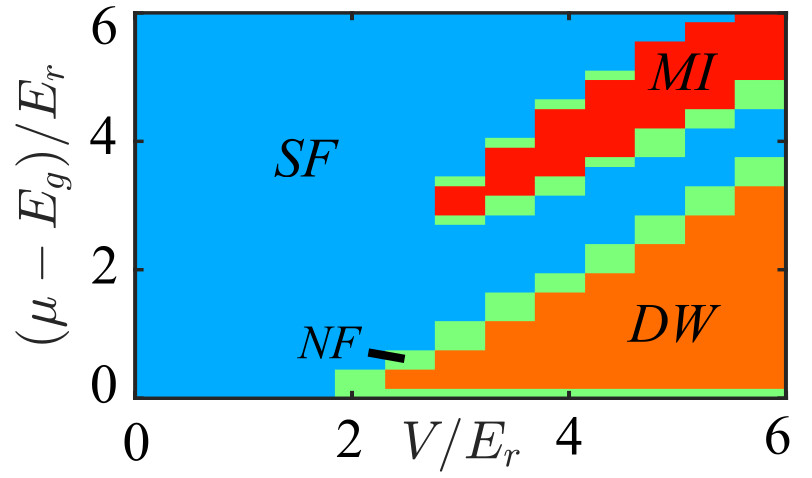
Abstract: A controlled twist between different underlying lattices allows one to interpolate, under a unified framework, across ordered and (quasi-)disordered matter while drastically changing quantum transport properties. Here, we use quantum Monte Carlo simulations to determine the unique phase diagrams of strongly-correlated ultracold bosons in twisted optical potentials. We show that at commensurate twisting angles, spectral gaps govern the formation of insulating patterns, separated by thin superfluid domains. The latter form weak superfluids, which are very sensitive to thermal fluctuations, but can be stabilized under appropriate parameter control. In contrast, slightly changing the twisting angle to a incommensurate value destroys most spectral gaps, leaving behind a prominent Bose glass phase. Our results are directly applicable to current generation experiments that quantum simulate moire physics.
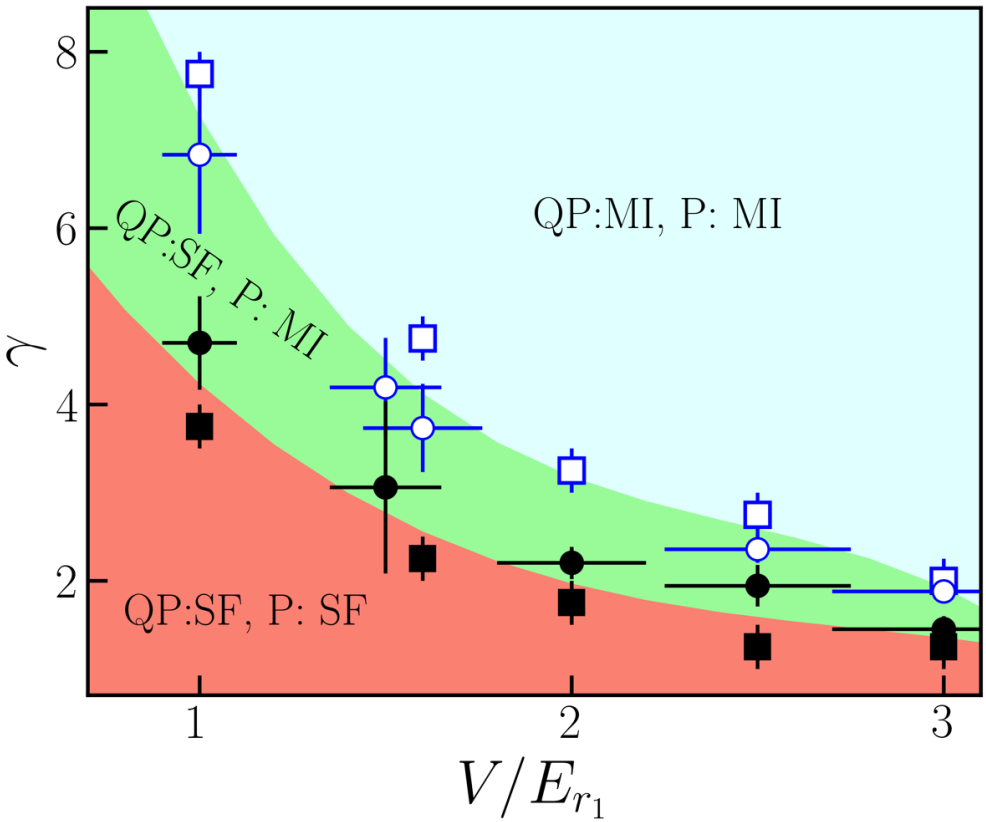
Abstract: Disorder or quasi-disorder is known to favor the localization in many-body Bose systems. Here in contrast, we demonstrate an anomalous delocalization effect induced by incommensurability in quasiperiodic lattices. Loading ultracold atoms in two shallow periodic lattices with equal amplitude and either equal or incommensurate spatial periods, we show the onset of a Mott transition not only in the periodic case but also in the quasiperiodic case. Upon increase of the incommensurate component of the potential we find that the Mott insulator turns into a delocalized superfluid. Our experimental results agree with quantum Monte Carlo calculations, showing anomalous delocalization induced by the interplay between the commensuration and interaction.
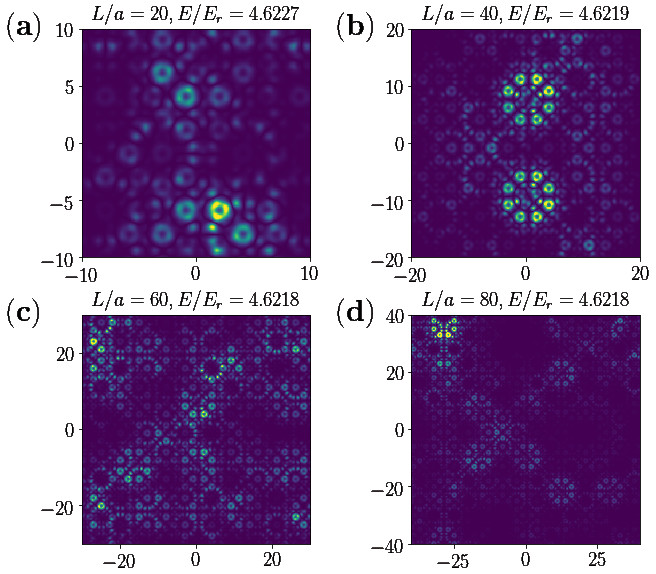
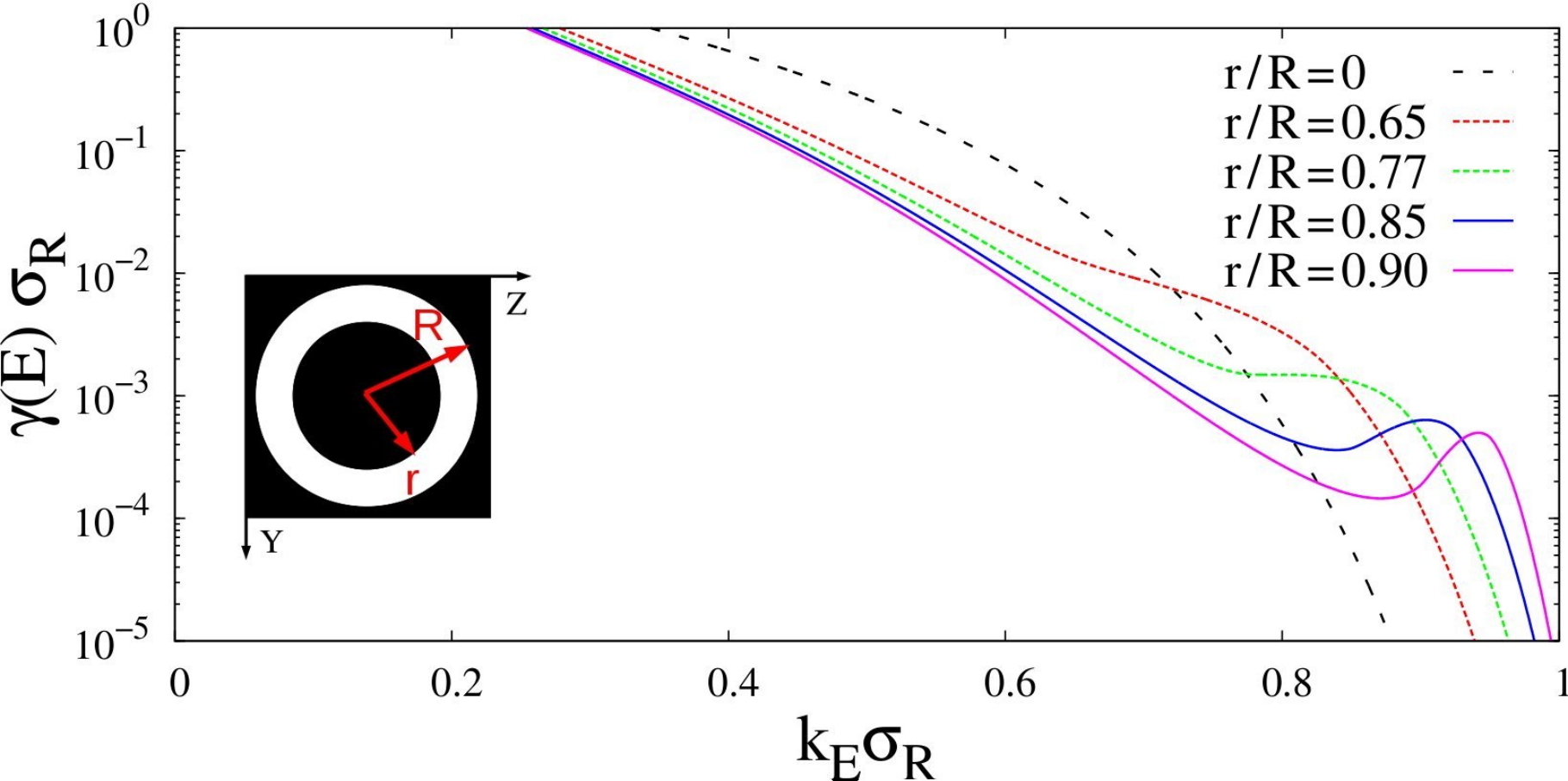
Abstract: Quasicrystals, a fascinating class of materials with long-range but nonperiodic order, have revolutionized our understanding of solid-state physics due to their unique properties at the crossroads of long-range-ordered and disordered systems. Since their discovery, they continue to spark broad interest for their structural and electronic properties. The quantum simulation of quasicrystals in synthetic quantum matter systems offers a unique playground to investigate these systems with unprecedented control parameters. Here, we investigate the localization properties and spectral structure of quantum particles in 2D quasicrystalline optical potentials. While states are generally localized at low energy and extended at high energy, we find alternating localized and critical states at intermediate energies. Moreover, we identify a complex succession of gaps in the energy spectrum. We show that the most prominent gap arises from strongly localized ring states, with the gap width determined by the energy splitting between states with different quantized winding numbers. In addition, we find that these gaps are stable for quasicrystals with different rotational symmetries and potential depths, provided that other localized states do not enter the gap generated by the ring states. Our findings shed light on the unique properties of quantum quasicrystals and have implications for their many-body counterparts.
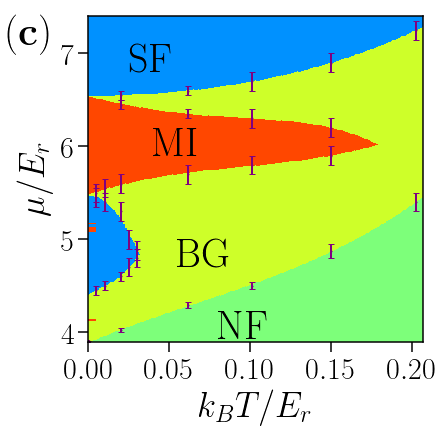
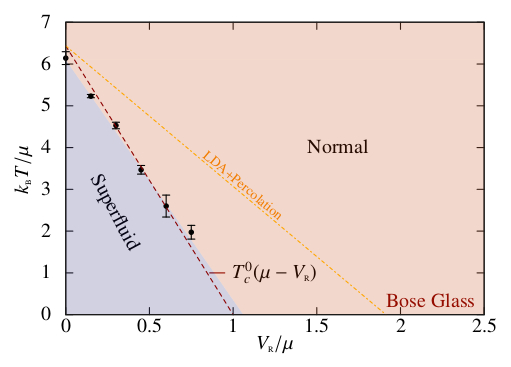
Abstract: Quantum simulation of quasicrystals in synthetic bosonic matter now paves the way for the exploration of these intriguing systems in wide parameter ranges. Yet thermal fluctuations in such systems compete with quantum coherence and significantly affect the zero-temperature quantum phases. Here we determine the thermodynamic phase diagram of interacting bosons in a two-dimensional, homogeneous quasicrystal potential. We find our results using quantum Monte Carlo simulations. Finite-size effects are carefully taken into account and the quantum phases are systematically distinguished from thermal phases. In particular, we demonstrate stabilization of a genuine Bose glass phase against the normal fluid in sizable parameter ranges. We interpret our results for strong interactions using a fermionization picture and discuss experimental relevance.
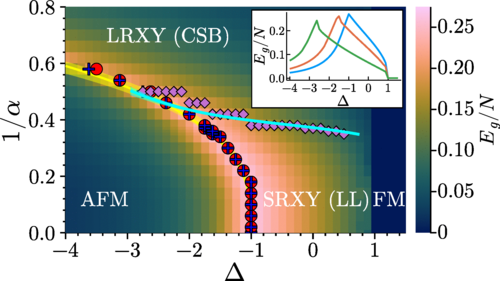
Abstract: Entanglement is a central feature of many-body quantum systems and plays a unique role in quantum phase transitions. In many cases, the entanglement spectrum, which represents the spectrum of the density matrix of a bipartite system, contains valuable information beyond the sole entanglement entropy. Here we investigate the entanglement spectrum of the long-range XXZ model. We show that within the critical phase it exhibits a remarkable self-similarity. The breakdown of self-similarity and the transition away from a Luttinger liquid is consistent with renormalization group theory. Combining the two, we are able to determine the quantum phase diagram of the model and locate the corresponding phase transitions. Our results are confirmed by numerically-exact calculations using tensor-network techniques. Moreover, we show that the self-similar rescaling extends to the geometrical entanglement as well as the Luttinger parameter in the critical phase. Our results pave the way to further studies of entanglement properties in long-range quantum models.
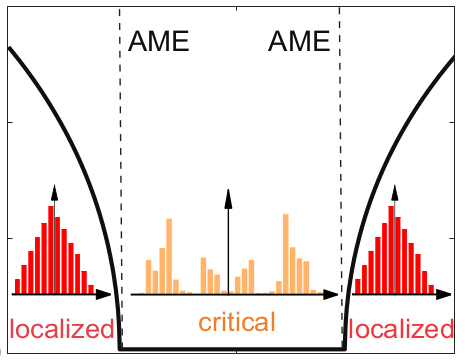
Abstract: Mobility edges, separating localized from extended states, are known to arise in the single-particle energy spectrum of disordered systems in dimension strictly higher than two and certain quasiperiodic models in one dimension. Here we unveil a different class of mobility edges, dubbed anomalous mobility edges, that separate bands of localized states from bands of critical states in diagonal and off-diagonal quasiperiodic models. We first introduce an exactly solvable quasi-periodic diagonal model and analytically demonstrate the existence of anomalous mobility edges. Moreover, numerical multifractal analysis of the corresponding wave functions confirms the emergence of a finite band of critical states. We then extend the sudy to a quasiperiodic off-diagonal Su-Schrieffer-Heeger model and show numerical evidence of anomalous mobility edges. We finally discuss possible experimental realizations of quasi-periodic models hosting anomalous mobility edges. These results shed new light on the localization and critical properties of low-dimensional systems with aperiodic order.
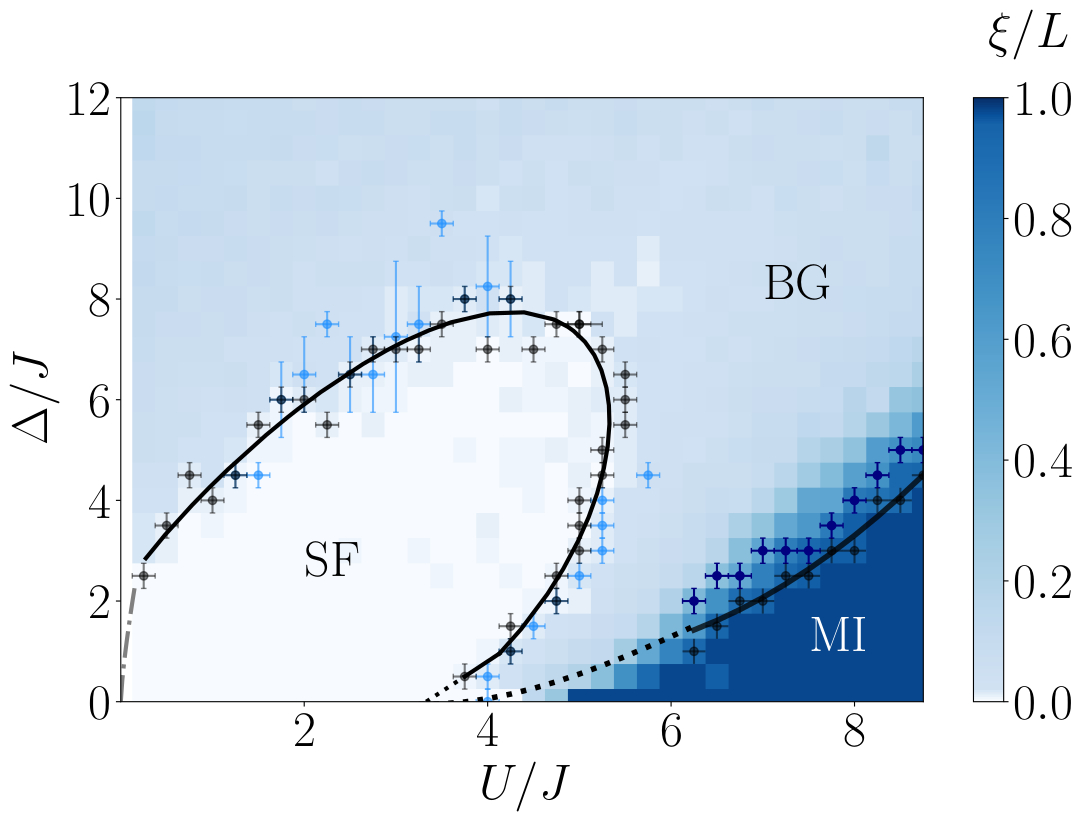
Abstract: The question of how the low-energy properties of disordered quantum systems may be connected to exotic localization phenomena at high energy is a key open question in the context of quantum glasses and many-body localization. In arXiv:2105.05774 we have shown that key features of the excitation spectrum of a disordered system can be efficiently probed from out-of-equilibrium dynamics following a quantum quench, providing distinctive signatures of the various phases. Here, we extend this work by providing a more in-depth study of the behavior of the quench spectral functions associated to different observables and investigating an extended parameter regime. We provide a detailed introduction to quench spectroscopy for disordered systems and show how spectral properties can be probed using both local operators and two-point correlation functions. We benchmark the technique using the one-dimensional Bose-Hubbard model in the presence of a random external potential, focusing on the low-lying excitations, and demonstrate that quench spectroscopy can distinguish the Mott insulator, superfluid, and Bose glass phases. We then explicitly reconstruct the zero-temperature phase diagram of the disordered Bose-Hubbard at fixed filling using two independent methods, both experimentally accessible via time-of-flight imaging and quantum gas microscopy respectively, and demonstrate that quench spectroscopy can give valuable insights as to the distribution of rare regions within disordered systems.s
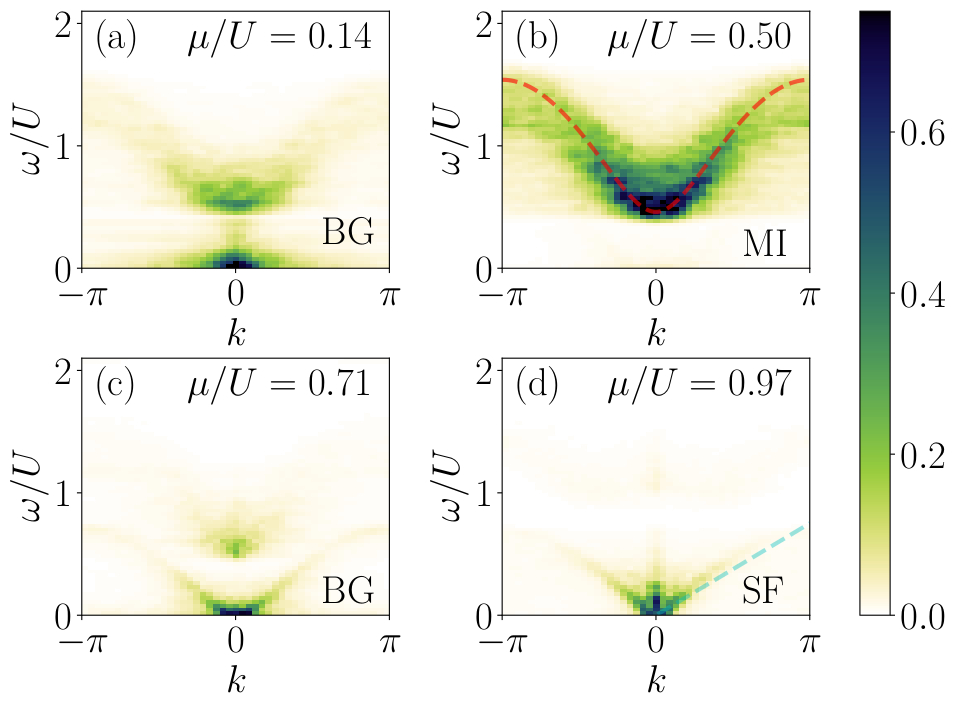
Abstract: The characterization of excitations in disordered quantum systems is a central issue in connection with glass physics and many-body localization. Here, we show that quench spectroscopy of a disordered model, as realized from its out-of-equilibrium dynamics following a global quench, allows us to fully characterize the spectral properties of the disordered phases. In the Bose-Hubbard model, a clear signature of gapless excitations in momentum-resolved spectroscopy enables us to accurately locate the Mott insulator to Bose glass transition, while the presence or absence of a well-defined soundlike mode distinguishes the superfluid from the Bose glass phase. Moreover, spatially-resolved spectroscopy provides local spectral properties and allows us to extract the typical spacing of gapless regions, giving a second independent way to uniquely identify all three phases. Our findings have far-ranging implications for a variety of experimental platforms, and offer a powerful and versatile probe of the low-energy phases of disordered systems.
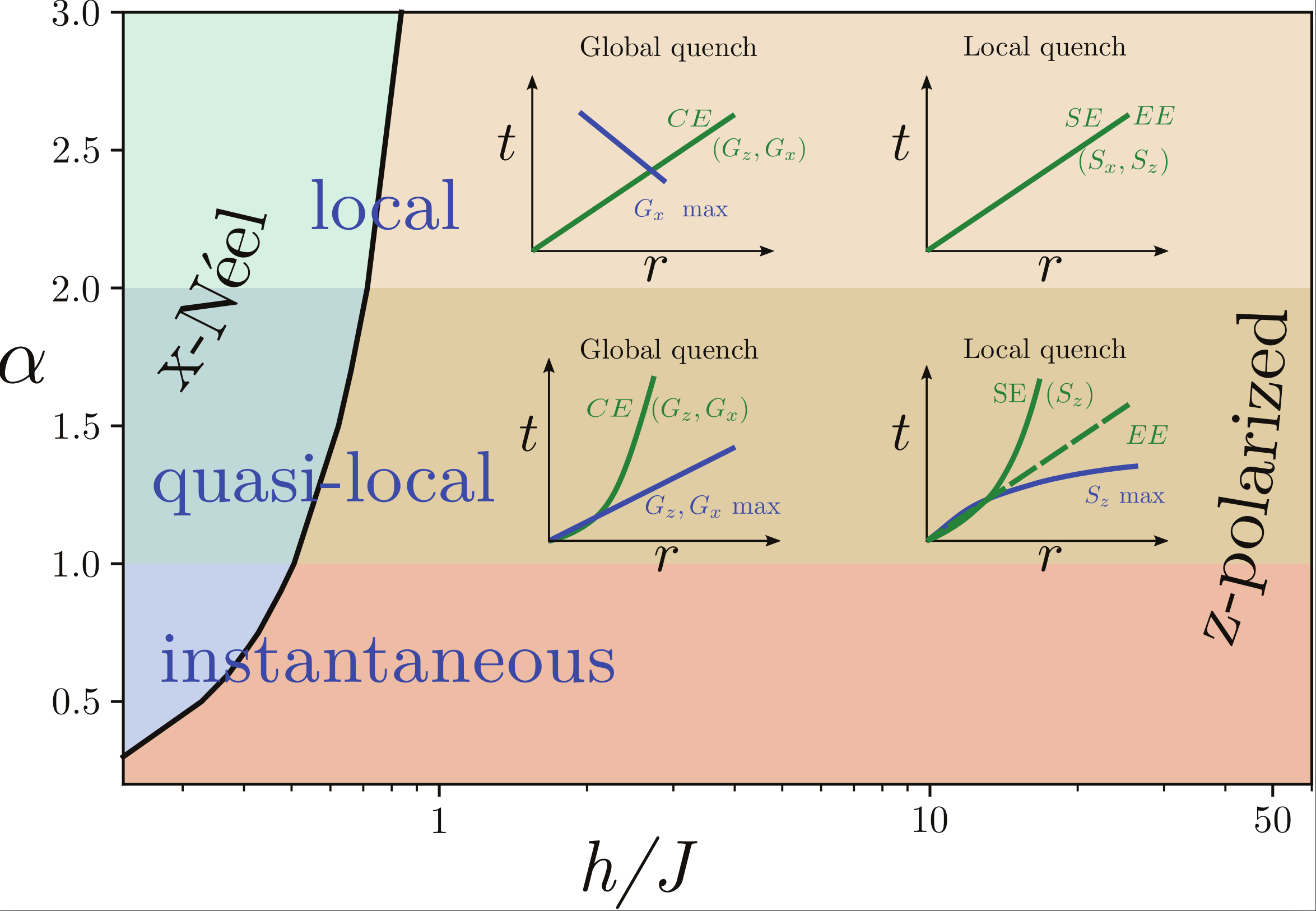
Abstract: Whether long-range interactions allow for a form of causality in non-relativistic quantum models remains an open question with far-reaching implications for the propagation of information and thermalization processes. Here, we study the out-of-equilibrium dynamics of the one-dimensional transverse Ising model with algebraic long-range exchange coupling. Using a state of the art tensor-network approach, complemented by analytic calculations and considering various observables, we show that a weak form of causality emerges, characterized by non-universal dynamical exponents. While the local spin and spin correlation causal edges are sub-ballistic, the causal region has a rich internal structure, which, depending on the observable, displays ballistic or super-ballistic features. In contrast, the causal region of entanglement entropy is featureless and its edge is always ballistic, irrespective of the interaction range. Our results shed light on the propagation of information in long-range interacting lattice models and pave the way to future experiments, which are discussed.

Abstract: Quasicrystals exhibit exotic properties inherited from the self-similarity of their long-range ordered, yet aperiodic, structure. The recent realization of an optical quasicrystal lattice for ultracold atoms paves the way to the study of correlated bosons in such structures, but the regime of strong interactions remains largely unexplored. Here, we determine the quantum phase diagram of two-dimensional correlated bosons in a quasicrystal potential. Using large-scale Monte Carlo calculations, we find evidence of a superfluid-to-Bose glass transition, and determine the critical line. Moreover, we show that strong interactions can stabilize a Mott insulator phase, possibly with spontaneously broken eightfold symmetry. Our results drive prospects to experimental investigation and, in particular, to the observation of the still elusive Bose glass phase in two dimensions.
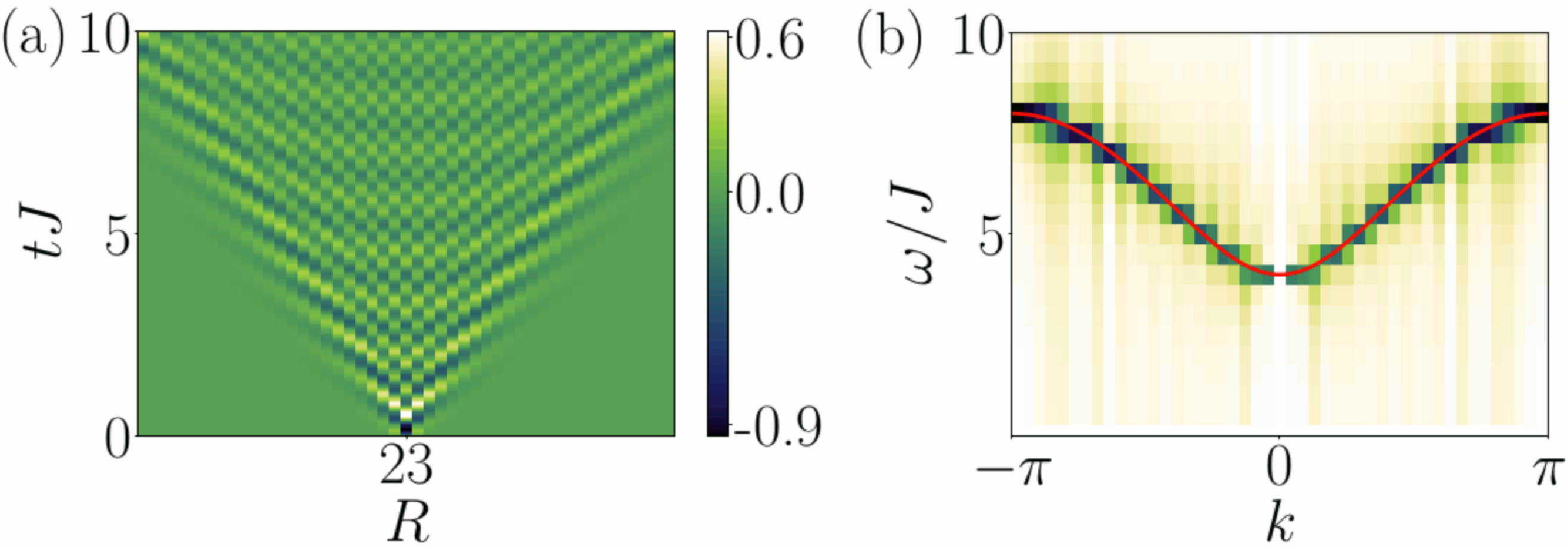
Abstract: Quench spectroscopy is a relatively new method which enables the investigation of spectral properties of many-body quantum systems by monitoring the out-of-equilibrium dynamics of real-space observables after a quench. So far the approach has been devised for global quenches or using local engineering of momentum-resolved excitations. Here, we extend the quench spectroscopy method to local quenches. We show that it allows us to extract quantitative information about global properties of the system, and in particular the elementary excitation spectrum. Using state-of-the-art numerical methods, we simulate the out-of-equilibrium dynamics of a variety of quantum systems following various local quench protocols and demonstrate a general scheme for designing an appropriate local quench protocol for any chosen model. We provide detailed examples of how the local quench protocol can be realised in realistic current generation experiments, including ultracold atomic gases and trapped ion systems.
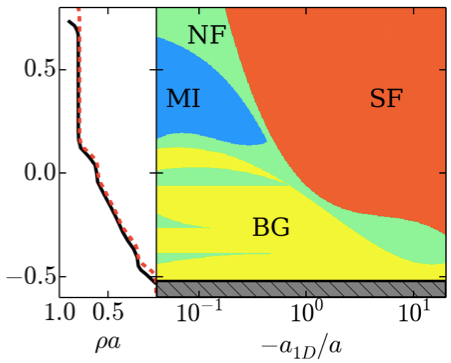
Abstract: The emergence of a compressible insulator phase, known as the Bose glass, is characteristic of the interplay of interactions and disorder in correlated Bose fluids. While widely studied in tight-binding models, its observation remains elusive owing to stringent temperature effects. Here we show that this issue may be overcome by using Lieb-Liniger bosons in shallow quasiperiodic potentials. A Bose glass, surrounded by superfluid and Mott phases, is found above a critical potential and for finite interactions. At finite temperature, we show that the melting of the Mott lobes is characteristic of a fractal structure and find that the Bose glass is robust against thermal fluctuations up to temperatures accessible in quantum gases. Our results raise questions about the universality of the Bose glass transition in such shallow quasiperiodic potentials.
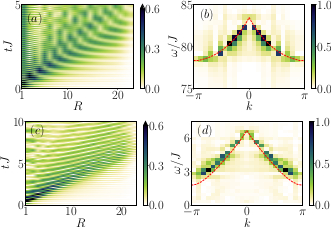
Abstract: Quenches are now routinely used in synthetic quantum systems to study a variety of fundamental effects, including ergodicity breaking, light-cone-like spreading of information, and dynamical phase transitions. It was shown recently that the dynamics of equal-time correlators may be related to ground-state phase transitions and some properties of the system excitations. Here, we show that the full low-lying excitation spectrum of a generic many-body quantum system can be extracted from the after-quench dynamics of equal-time correlators. We demonstrate it for a variety of one-dimensional lattice models amenable to exact numerical calculations, including Bose and spin models, with short or long range interactions. The approach also applies to higher dimensions, correlated fermions, and continuous models. We argue that it provides an alternative approach to standard pump-probe spectroscopic methods and discuss its advantages
Abstract: We study the elastic scattering time Ï s of ultracold atoms propagating in optical disordered potentials in the strong scattering regime, going beyond the recent work of J. Richard et al. Phys. Rev. Lett. 122 100403 (2019). There, we identified the crossover between the weak and the strong scattering regimes by comparing direct measurements and numerical simulations to the first order Born approximation. Here we focus specifically on the strong scattering regime, where the first order Born approximation is not valid anymore and the scattering time is strongly influenced by the nature of the disorder. To do so, we connect our observations of Ï s to the profiles of the spectral functions that we estimate using higher order Born perturbation theory or self-consistent Born approximation. The comparison reveals that self-consistent methods are well suited to describe Ï s for Gaussian-distributed disorder, but fails for laser speckle disorder. For the latter, we show that the peculiar profiles of the spectral functions, as measured independently in V. Volchkov et al. Phys. Rev. Lett. 120, 060404 (2018), must be taken into account. Altogether our study characterizes the validity range of usual theoretical methods to predict the elastic scattering time of matter waves, which is essential for future close comparison between theory and experiments, for instance regarding the ongoing studies on Anderson localization.
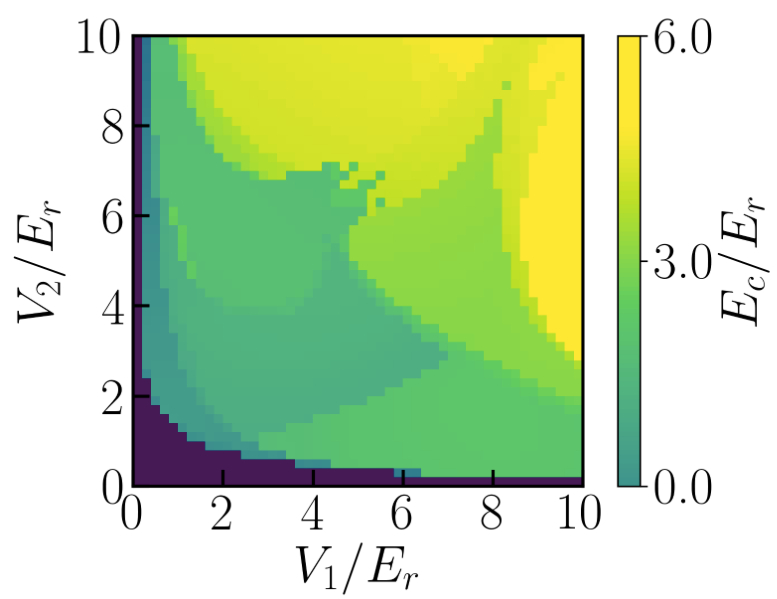
Abstract: Quasi-periodic systems offer an appealing intermediate between long-range ordered and genuine disordered systems, with unusual critical properties. One-dimensional models that break the so-called self-dual symmetry usually display a mobility edge, similarly as truly disordered systems in dimension strictly higher than two. Here, we determine the critical localization properties of single particles in shallow, one-dimensional, quasi-periodic models, and relate them to the fractal character of the energy spectrum. On the one hand, we determine the mobility edge and show that it separates the localized and extended phases, with no intermediate phase. On the other hand, we determine the critical potential amplitude and find the universal critical exponent nuâ1/3. We also study the spectral Hausdorff dimension and show that it is non-universal but always smaller than unity, hence showing that the spectrum is point-like. Finally, applications to on-going studies of Anderson localization, Bose glass physics, and many-body localization in ultracold atoms are discussed.
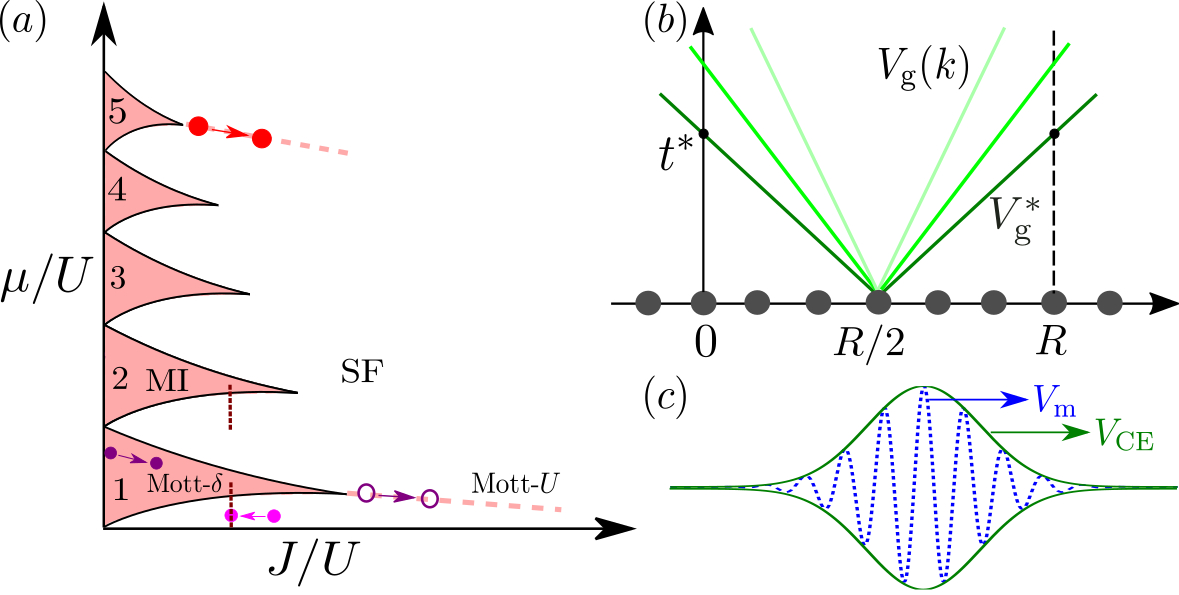
Abstract: We study the spreading of correlations in the Bose-Hubbard chain, using the time-dependent matrix-product state approach. In both the superfluid and the Mott-insulator phases, we find that the time-dependent correlation functions generally display a universal twofold cone structure characterized by two distinct velocities. The latter are related to different microscopic properties of the system and provide useful information on the excitation spectrum. The twofold spreading of correlations has profound implications on experimental observations that are discussed.
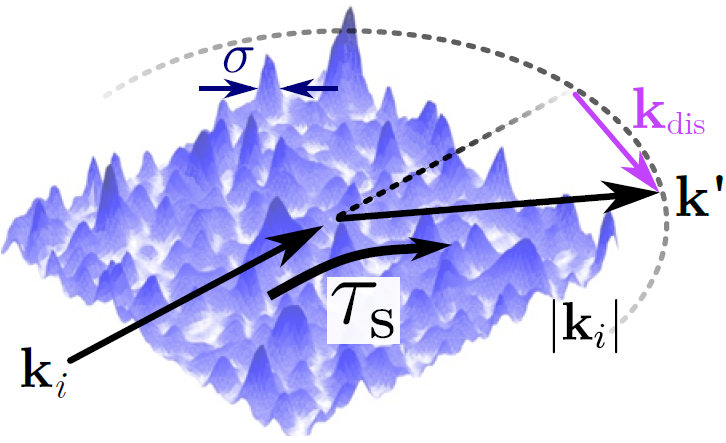
Abstract: We report on the direct measurement of the elastic scattering time $ au_ extrm{s}$ of ultracold atoms propagating in optical disordered potentials. By exploring this fundamental quantity over a large range of experimental parameters, we observe variations of $ au_ extrm{s}$ over more than three orders of magnitude, in excellent agreement with numerical calculations. It allows us to study the crossover from the weak to the strong scattering regimes, which are explicitly identified by a comparison to the first order Born approximation. We especially discuss the relevance of the widely used criterion $k imes l_ extrm{s}$ to locate this crossover. While it is validated for a Gaussian disorder, it breaks down for the laser speckle disorders used in the experiments, where large deviations to Born predictions are observed. This result highlights the strong influence of the disorder statistics on the crossover and, more generally, on the behavior of the time $ au_ extrm{s}$ in the strong scattering regime.
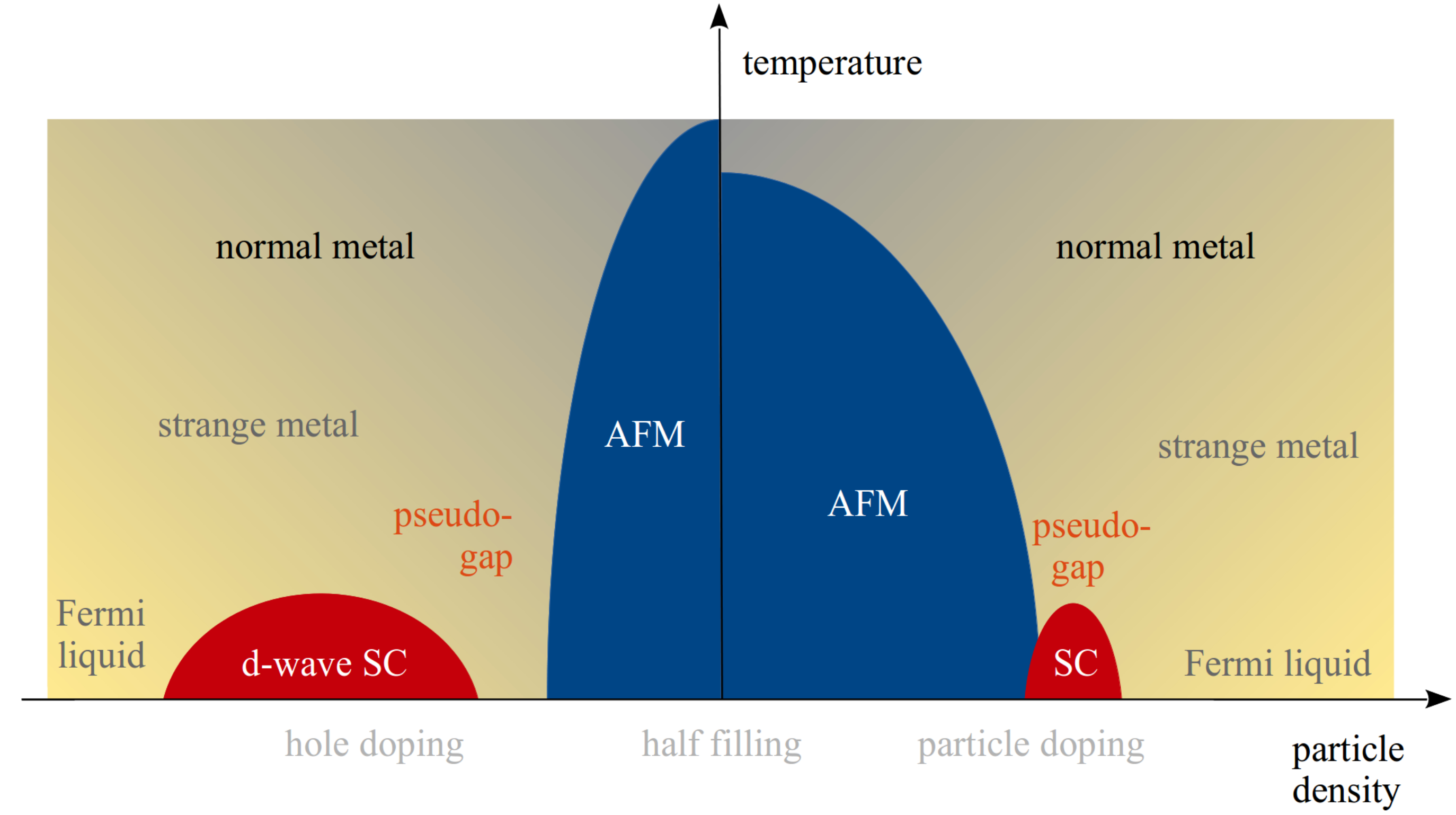
Abstract: Ultracold atomic gases provide a fantastic platform to implement quantum simulators and investigate a variety of models initially introduced in condensed matter physics or other areas. One of the most promissing applications of quantum simulation is the study of strongly-correlated Fermi gases, for which exact theoretical results are not always possible with state-of-the-art approaches. Here, we review recent progress of the quantum simulation of the emblematic Fermi-Hubbard model with ultracold atoms. After introducing the Fermi-Hubbard model in the context of condensed matter, its implementation in ultracold atom systems, and its phase diagram, we review landmark experimental achievements, from the early observation of the onset of quantum degeneracy and superfluidity to demonstration of the Mott insulator regime and the emergence of long-range anti-ferromagnetic order. We conclude by discussing future challenges, including the possible observation of high-Tc superconductivity, transport properties, and the interplay of strong correlations and disorder or toplogy.

Abstract: Envisioned by Richard Feynman in the early 1980s, quantum simulation has received dramatic impetus thanks to the development of a variety of plateforms able to emulate a wide class of quantum Hamiltonians. During the past decade, most of the quantum simulators have implemented rather well-known models, hence permitting a direct comparison with theoretical calculations and a precise benchmarking of their reliability. The field has now reached a maturity such that one can address difficult problems, which cannot be solved efficiently using classical algorithms. These advances provide unprecedented opportunities to explore previously unreachable fields, test theoretical predictions, and inspire novel approaches. This contribution is an introduction to quantum simulation. It is published as a forward to the special issue on Quantum Simulation of the Comptes-Rendus de Physique of the French Academy of Sciences.
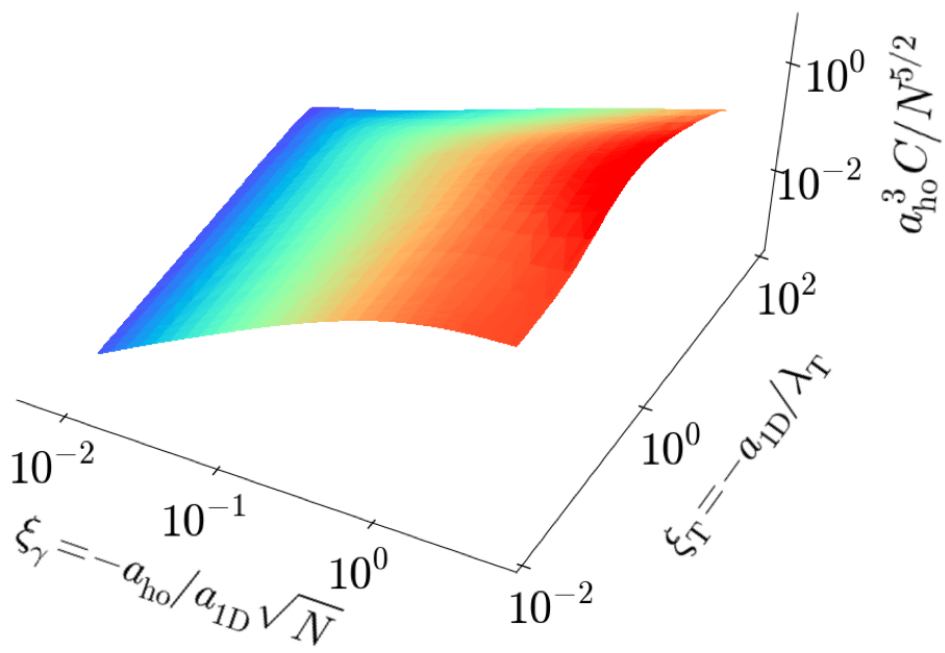
Abstract: The universal Tan relations connect a variety of microscopic features of many-body quantum systems with two-body contact interactions to a single quantity, called the contact. The latter has become pivotal in the description of quantum gases. We provide a complete characterization of the Tan contact of the harmonically trapped Lieb-Liniger gas for arbitrary interactions and temperature. Combining thermal Bethe ansatz, local density approximation, and exact quantum Monte Carlo calculations, we show that the contact is a universal function of only two scaling parameters, and determine the scaling function. We find that the temperature-dependence of the contact, or equivalently the interaction-dependence of the entropy, displays a maximum. The presence of this maximum provides an unequivocal signature of the crossover to the fermionized regime and it is accessible in current experiments.
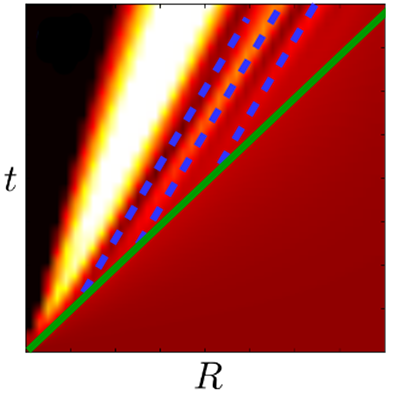
Abstract: The spreading of correlations after a quantum quench is studied in a wide class of lattice systems, with short- and long-range interactions. Using a unifying quasiparticle framework, we unveil a rich structure of the correlation cone, which encodes the footprints of several microscopic properties of the system. When the quasiparticle excitations propagate with a bounded group velocity, we show that the correlation edge and correlation maxima move with different velocities that we derive. For systems with a divergent group velocity, especially relevant for long-range interacting systems, the correlation edge propagates slower than ballistic. In contrast, the correlation maxima propagate faster than ballistic in gapless systems but ballistic in gapped systems. Our results shed light on existing experimental and numerical observations and pave the way to the next generation of experiments. For instance, we argue that the dynamics of correlation maxima can be used as a witness of the elementary excitations of the system.
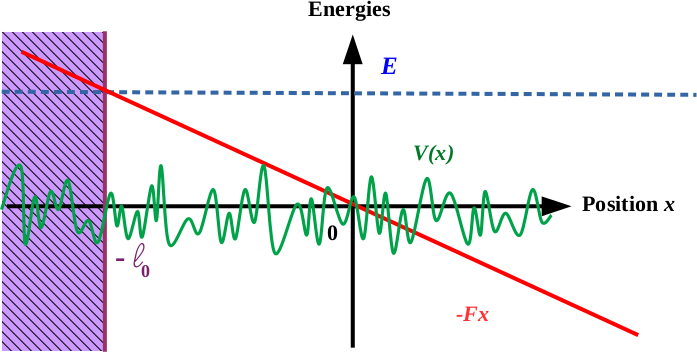
Abstract: We study numerically the expansion dynamics of an initially confined matter wave packet in the presence of a disordered potential and a uniform bias force. For white-noise disorder, we find that the wave packet develops asymmetric algebraic tails for any ratio of the force to the disorder strength. The exponent of the algebraic tails decays smoothly with that ratio and no evidence of a critical behavior on the wave density profile is found. Algebraic localization features a series of critical values of the force-to-disorder strength where the m-th position moment of the wave packet diverges. Below the critical value for the m-th moment, we find fair agreement between the asymptotic long-time value of the m-th moment and the predictions of diagrammatic calculations. Above it, we find that the m-th moment grows algebraically in time. For correlated disorder, we find evidence of systematic delocalization, irrespective to the model of disorder. More precisely, we find a two-step dynamics, where both the center-of-mass position and the width of the wave packet show transient localization, similar to the white-noise case, at short time and delocalization at sufficiently long time. This correlation-induced delocalization is interpreted as due to the decrease of the effective de Broglie wave length, which lowers the effective strength of the disorder in the presence of finite-range correlations.
Abstract: We introduce time-dependent variational Monte Carlo for continuous-space Bose gases. Our approach is based on the systematic expansion of the many-body wave-function in terms of multi- body correlations and is essentially exact up to adaptive truncation. The method is benchmarked by comparison to exact Bethe-ansatz or existing numerical results for the integrable Lieb-Liniger model. We first show that the many-body wave-function achieves high precision for ground-state properties, including energy and first-order as well as second-order correlation functions. Then, we study the out-of-equilibrium, unitary dynamics induced by a quantum quench in the interaction strength. Our time-dependent variational Monte Carlo results are benchmarked by comparison to exact Bethe ansatz results available for a small number of particles, and also compared to quench action results available for non-interacting initial states. Moreover, our approach allows us to study large particle numbers and general quench protocols, previously inaccessible beyond the mean-field level. Our results suggest that it is possible to find correlated initial states for which the long-term dynamics of local density fluctuations is close to the predictions of a simple Boltzmann ensemble.
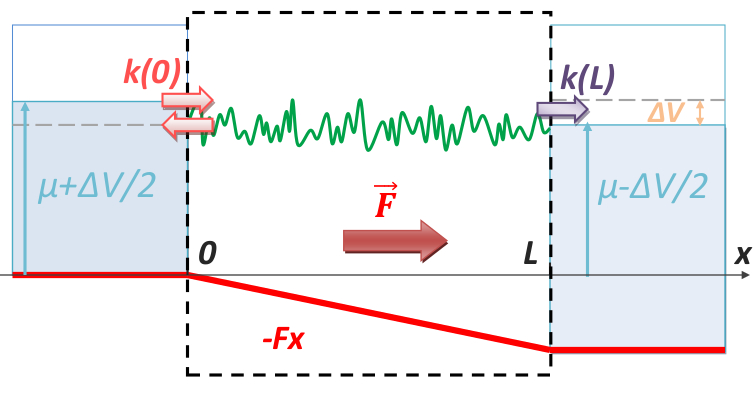
Abstract: We study the transmission of a disordered wave guide subjected to a finite bias field. The statistical distribution of transmission is analytically shown to take a universal form. It depends on a single parameter, the system length expressed in a rescaled metrics, which encapsulates all the microscopic features of the medium and the bias field. Excellent agreement with numerics is found for various models of disorder and bias field. For white-noise disorder and a linear bias field, we demonstrate the algebraic nature of the decay of the transmission with distance, irrespective of the value of the bias field. It contrasts with the expansion of a wave packet, which features a delocalization transition for large bias field. The difference is attributed to the different boundary conditions for the transmission and expansion schemes. The observability of these effects in conductance measurements for electrons or ultracold atoms is discussed, taking into account key features, such as finite-range disorder correlations, non-linear bias fields, and finite temperatures.
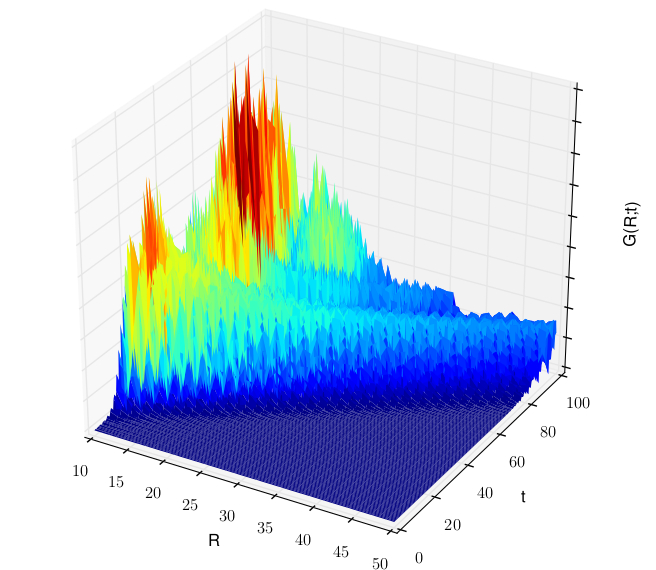
Abstract: We study the out-of-equilibrium dynamics induced by quantum quenches in quadratic Hamiltonians featuring both short- and long-range interactions. The spreading of correlations in the presence of algebraic decaying interactions, 1/R^a, is studied for lattice Bose models in arbitrary dimension D. These models are exactly solvable and provide useful insight in the universal description of more complex systems as well as comparisons to the known universal upper bounds for the spreading of correlations. Using analytical calculations of the dominant terms and full numerical integration of all quasi-particle contributions, we identify three distinct dynamical regimes. For strong decay of interactions, a>D+1, we find a causal regime, qualitatively similar to what previously found for short-range interactions. This regime is characterized by ballistic (linear cone) spreading of the correlations with a cone velocity equal to twice the maximum group velocity of the quasi-particles. For weak decay of interactions, D>a, we find instantaneous activation of correlations at arbitrary distance. This signals the breaking of causality, which can be associated with the divergence of the quasi-particle energy spectrum. Finite-size scaling of the activation time precisely confirms thisinterpretation. For intermediate decay of interactions, D+1>a>D, we find a sub-ballistic, algebraic (bent cone) spreading and determine the corresponding exponent as a function of a. These outcomes generalize existing results for one-dimensional systems to arbitrary dimension. We precisely relate the three regimes to the first- and second-order divergences of the quasi-particle energy spectrum for any dimension. The long-range transverse Ising model in dimensions D=1, 2, and 3 in the (quadratic) spin-wave approximation is more specifically studied and we also discuss the shape of the correlation front in dimension higher than one. Our results apply to several condensed-matter systems as well as atomic, molecular, and optical systems, and pave the way to the observation of causality and its breaking in diverse experimental realisation.
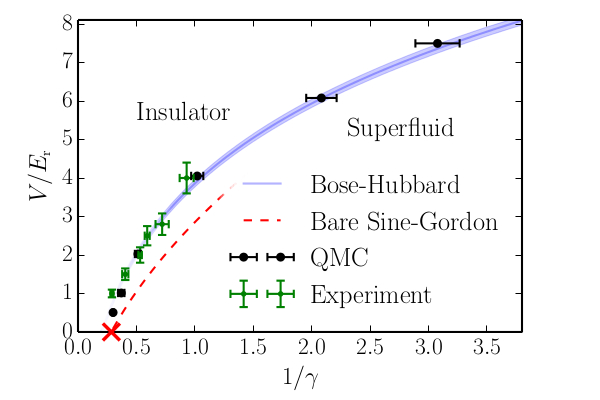
Abstract: We investigate the superfluid-insulator transition of one-dimensional interacting bosons in both deep and shallow periodic potentials. We compare a theoretical analysis based on quantum Monte-Carlo simulations in continuum space and Luttinger liquid approach with experiments on ultracold atoms with tunable interactions and optical lattice depth. Experiments and theory are in excellent agreement. Our study provides a quantitative determination of the critical parameters for the Mott transition and defines the regimes of validity of widely used approximate models, namely the Bose-Hubbard and sine-Gordon models.
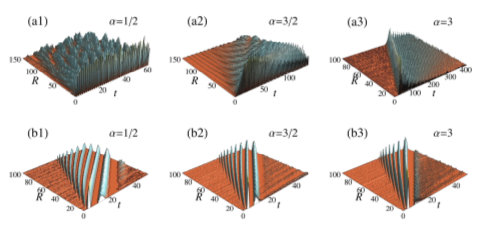
Abstract: We study the out-of-equilibrium dynamics of quantum systems with long-range interactions. Two different models describing, respectively, interacting lattice bosons and spins are considered. Our study relies on a combined approach based, on one hand, on accurate many-body numerical calculations and, on the other hand, on a quasi-particle microscopic theory. For sufficiently fast decaying long-range potentials, we find that the quantum speed limit set by the long-range Lieb-Robinson bounds is never attained and a purely ballistic behavior is found. For slowly decaying potentials, a radically different scenario is observed. In the bosonic case, a remarkable local spreading of correlations is still observed, despite the existence of infinitely fast traveling excitations in the system. This is in marked contrast with the spin case, where locality is broken. We finally provide a microscopic justification of the different regimes observed and of the origin of the protected locality in the bosonic model.
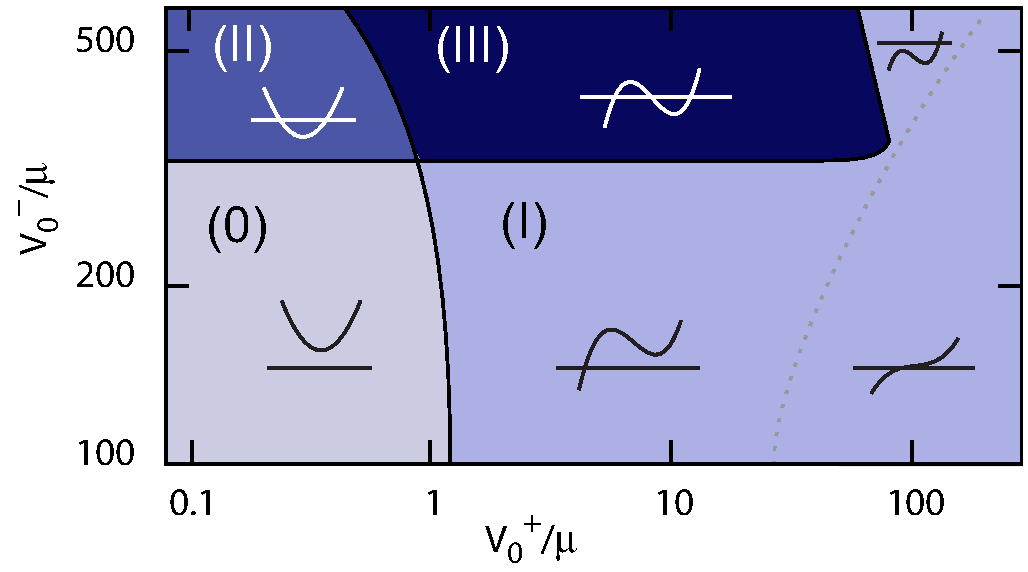
Abstract: We study the effect of disorder on the propagation of collective excitations in a disordered Bose superfluid. We incorporate local density depletion induced by strong disorder at the meanfield level, and formulate the transport of the excitations in terms of a screened scattering problem. We show that the competition of disorder, screening, and density depletion induces a strongly non-monotonic energy dependence of the disorder parameter. In three dimensions, it results in a rich localization diagram with four different classes of mobility spectra, characterized by either no or up to three mobility edges. Implications on experiments with disordered ultracold atoms are discussed.
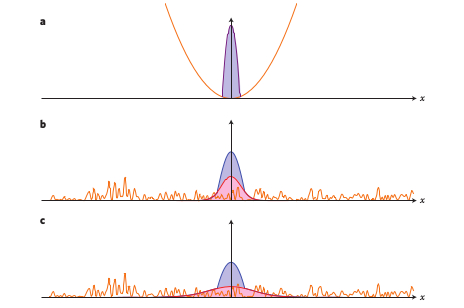
Abstract: The Anderson transition point between localization and diffusion - the mobility edge - has now been directly measured in an ultracold-atom experiment.
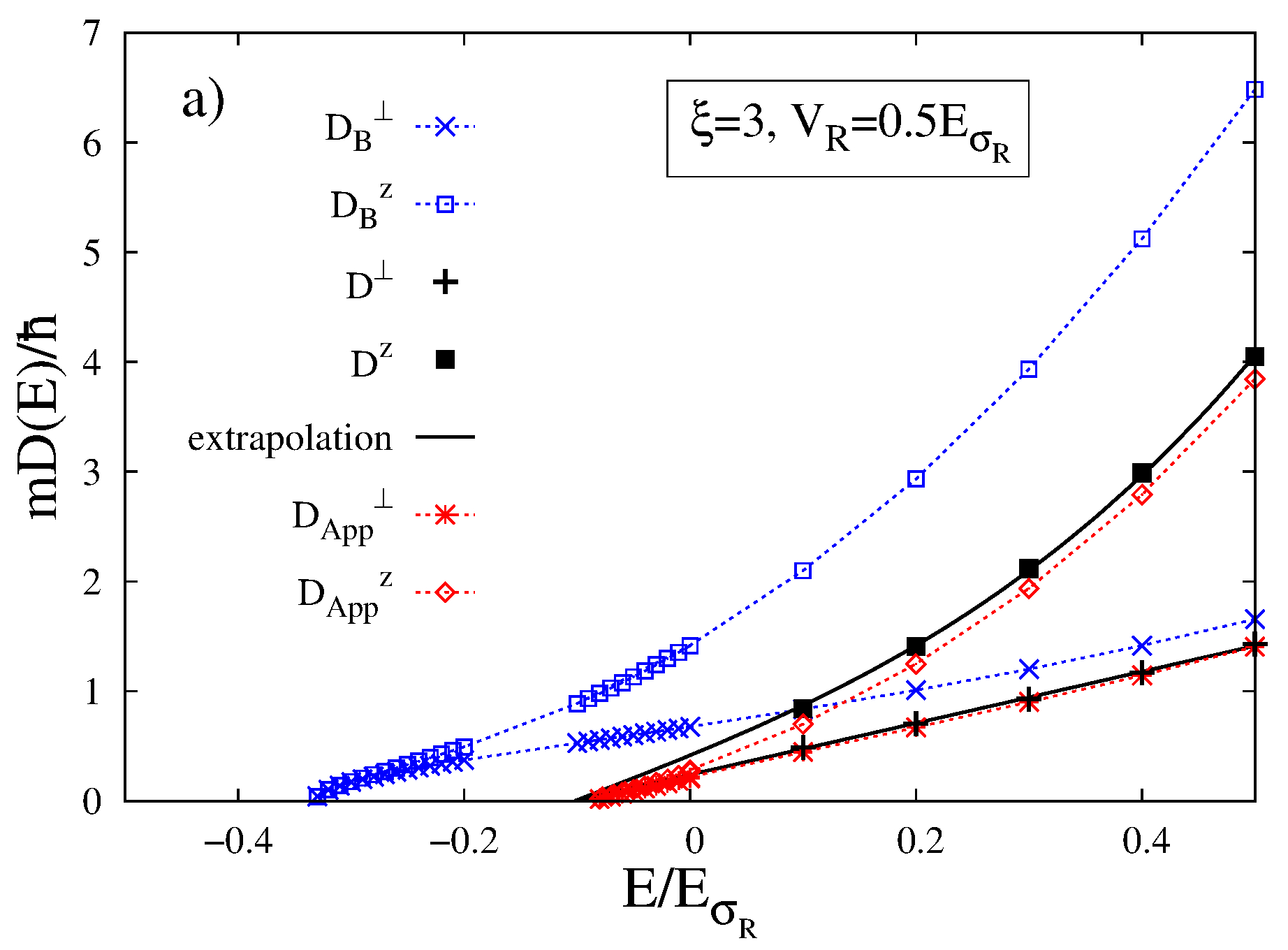
Abstract: Using a cut-off free formulation of the coherent transport theory, we show that the interference terms at the origin of localization strongly affect the transport anisotropy. In contrast to the common hypothesis, we then find that the anisotropies of incoherent and coherent diffusion are significantly different, in particular at criticality. There, we show that the coherent transport anisotropy is mainly determined by the properties of the disorder-averaged effective scattering medium while the incoherent transport contributions become irrelevant.
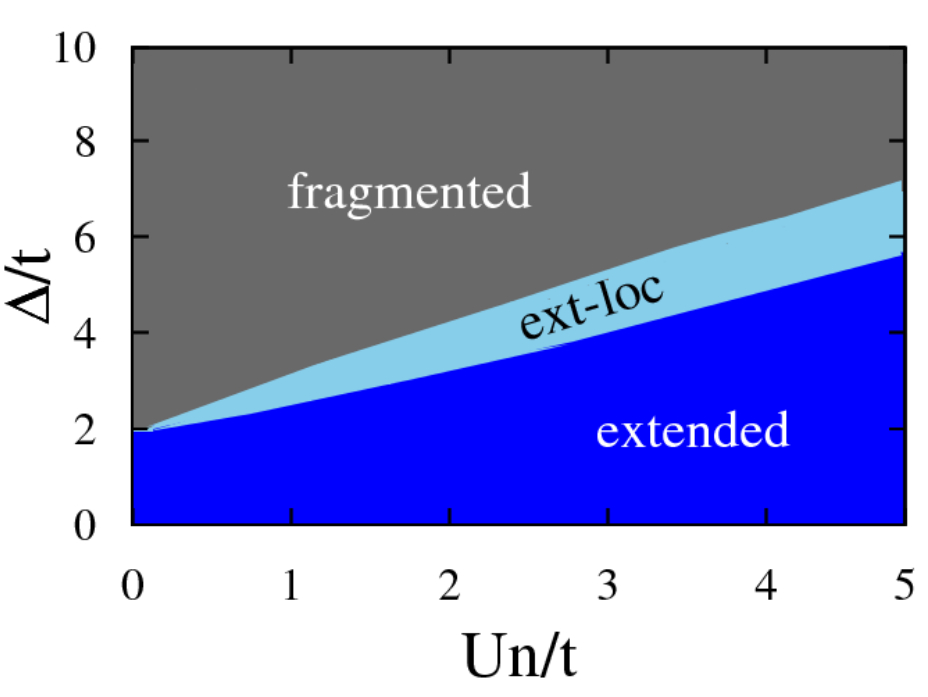
Abstract: We study the localization of collective pair excitations in weakly-interacting Bose superfluids in one-dimensional quasiperiodic lattices. The localization diagram is first determined numerically. For intermediate interaction and quasiperiodic amplitude we find a sharp localization transition, with extended low-energy states and localized high-energy states. We then develop an analytical treatment, which allows us to quantitatively map the localization transition into that of an effective multiharmonic quasiperiodic system.
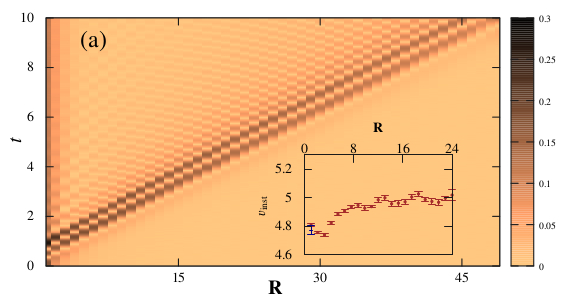
Abstract: We study the spreading of density-density correlations in Bose-Hubbard models after a quench of the interaction strength, using time-dependent variational Monte Carlo simulations. It gives access to unprecedented long propagation times and to dimensions higher than one. In both one and two dimensions, we find ballistic light-cone spreading of correlations and extract accurate values of the light-cone velocity in the superfluid regime. We show that the spreading of correlations is generally supersonic, with a light-cone propagating faster than sound modes but slower than the maximum group velocity of density excitations, except at the Mott transition, where all the characteristic velocities are equal. Further, we show that in two dimensions the correlation spreading is highly anisotropic and presents nontrivial interference effects.
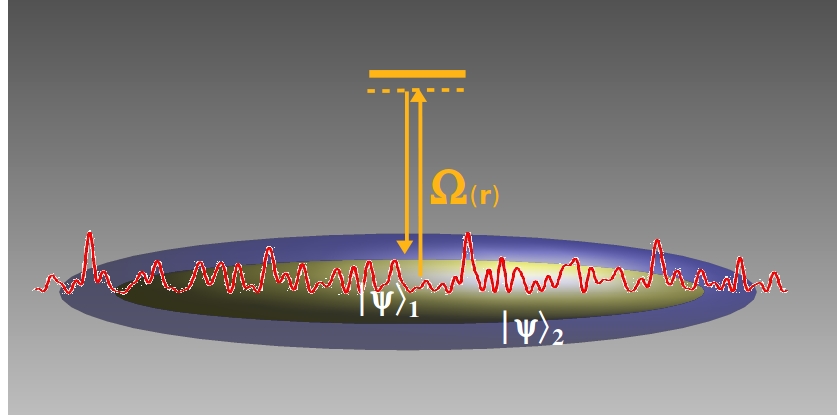
Abstract: We study the competition between one-body and two-body couplings in weakly-interacting two-component Bose gases, in particular as regards field correlations. We derive the meanfield theory for both ground state and low-energy pair excitations in the general case where both one-body and two-body couplings are position-dependent and the fluid is subjected to a state-dependent trapping potential. General formulas for phase and density correlations are also derived. Focusing on the case of homogeneous systems, we discuss the pair-excitation spectrum and the corresponding excitation modes, and use them to calculate correlation functions, including both quantum and thermal fluctuation terms. We show that the relative phase of the two components is imposed by that of the one-body coupling, while its fluctuations are determined by the modulus of the one-body coupling and by the two-body coupling. One-body coupling and repulsive two-body coupling cooperate to suppress relative-phase fluctuations, while attractive two-body coupling tends to enhance them. Further applications of the formalism presented here and extensions of our work are also discussed.
Abstract: We study the phase diagram of two-dimensional, interacting bosons in the presence of a correlated disorder in continuous space, using large-scale finite temperature quantum Monte Carlo simulations. We show that the superfluid transition is strongly protected against disorder. It remains of the Berezinskii-Kosterlitz-Thouless type up to disorder strengths comparable to the chemical potential. Moreover, we study the transport properties in the strong disorder regime where a zero-temperature Bose-glass phase is expected. We show that the conductance exhibits a thermally activated behavior vanishing only at zero temperature. Our results point towards the existence of Bose bad-metal phase as a precursor of the Bose-glass phase.
Abstract: The macroscopic transport properties in a disordered potential, namely diffusion and weak/strong localization, closely depend on the microscopic and statistical properties of the disorder itself. This dependence is rich of counter-intuitive consequences. It can be particularly exploited in matter wave experiments, where the disordered potential can be tailored and controlled, and anisotropies are naturally present. In this work, we apply a perturbative microscopic transport theory and the self-consistent theory of Anderson localization to study the transport properties of ultracold atoms in anisotropic 2D and 3D speckle potentials. In particular, we discuss the anisotropy of single-scattering, diffusion and localization. We also calculate a disorder-induced shift of the energy states and propose a method to include it, which amounts to renormalize energies in the standard on-shell approximation. We show that the renormalization of energies strongly affects the prediction for the 3D localization threshold (mobility edge). We illustrate the theoretical findings with examples which are revelant for current matter wave experiments, where the disorder is created with a laser speckle. This paper provides a guideline for future experiments aiming at the precise location of the 3D mobility edge and study of anisotropic diffusion and localization effects in 2D and 3D.
Abstract: We study Anderson localization of single particles in continuous, correlated, one-dimensional disordered potentials. We show that tailored correlations can completely change the energy-dependence of the localization length. By considering two suitable models of disorder, we explicitly show that disorder correlations can lead to a nonmonotonic behavior of the localization length versus energy. Numerical calculations performed within the transfer-matrix approach and analytical calculations performed within the phase formalism up to order three show excellent agreement and demonstrate the effect. We finally show how the nonmonotonic behavior of the localization length with energy can be observed using expanding ultracold-atom gases.
Abstract: We show that, in contrast to immediate intuition, Anderson localization of noninteracting particles induced by a disordered potential in free space can increase (i.e., the localization length can decrease) when the particle energy increases, for appropriately tailored disorder correlations. We predict the effect in one, two, and three dimensions, and propose a simple method to observe it using ultracold atoms placed in optical disorder. The increase of localization with the particle energy can serve to discriminate quantum versus classical localization.
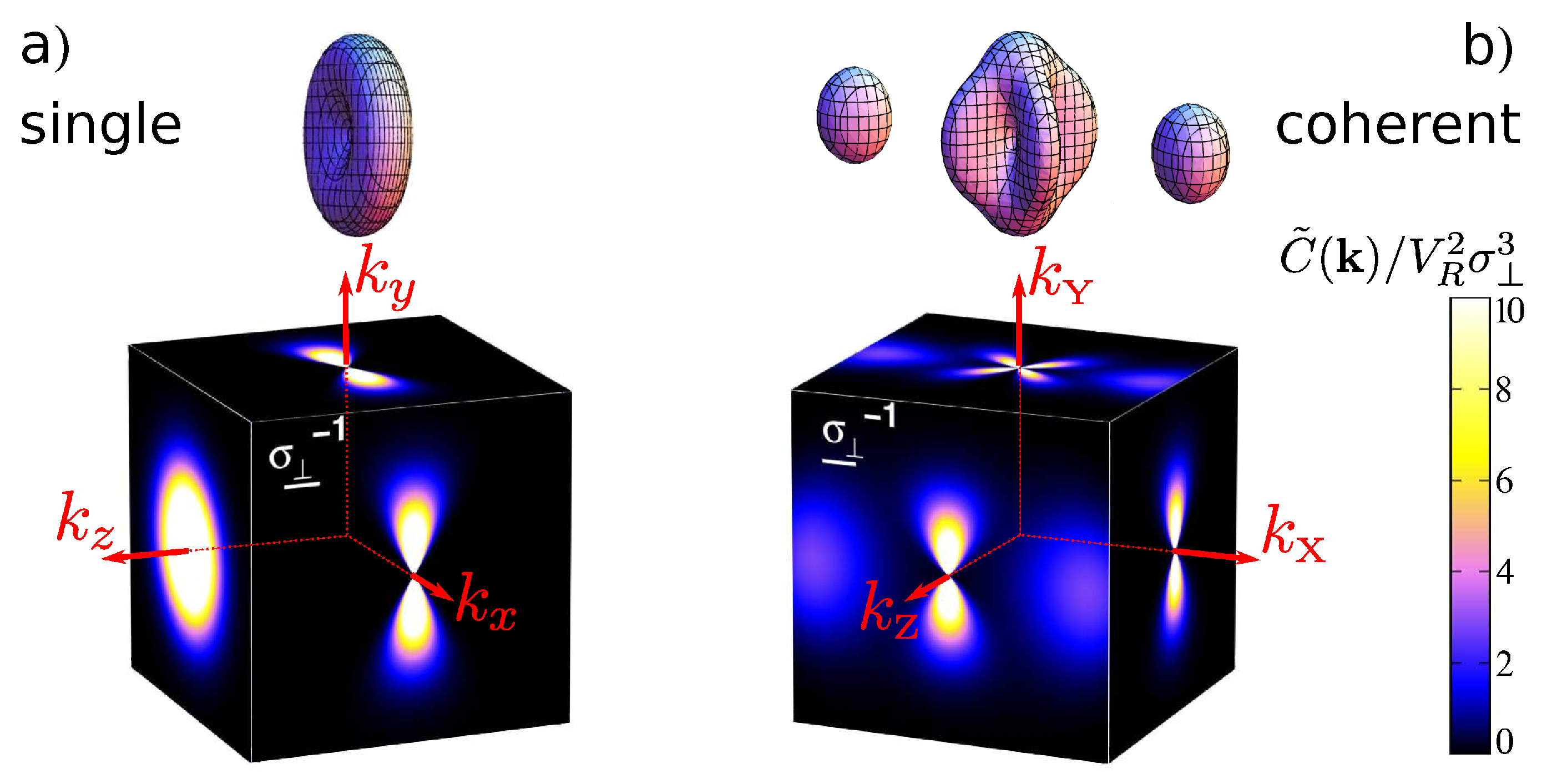
Abstract: We study quantum transport in anisotropic 3D disorder and show that non rotation invariant correlations can induce rich diffusion and localization properties. For instance, structured finite-range correlations can lead to the inversion of the transport anisotropy. Moreover, working beyond the self-consistent theory of localization, we include the disorder-induced shift of the energy states and show that it strongly affects the mobility edge. Implications to recent experiments are discussed.

Abstract: In disordered media, quantum interference effects are expected to induce complete suppression of electron conduction. The phenomenon, known as Anderson localization, has a counterpart with classical waves that has been observed in acoustics, electromagnetism and optics, but a direct observation for particles remains elusive. Here, we report the observation of the three-dimensional localization of ultracold atoms in a disordered potential created by a speckle laser field. A phenomenological analysis of our data distinguishes a localized component of the resulting density profile from a diffusive component. The observed localization cannot be interpreted as the classical trapping of particles with energy below the classical percolation threshold in the disorder, nor can it be understood as quantum trapping in local potential minima. Instead, our data are compatible with the self-consistent theory of Anderson localization tailored to our system, involving a heuristic energy shift that offers scope for future interpretation.
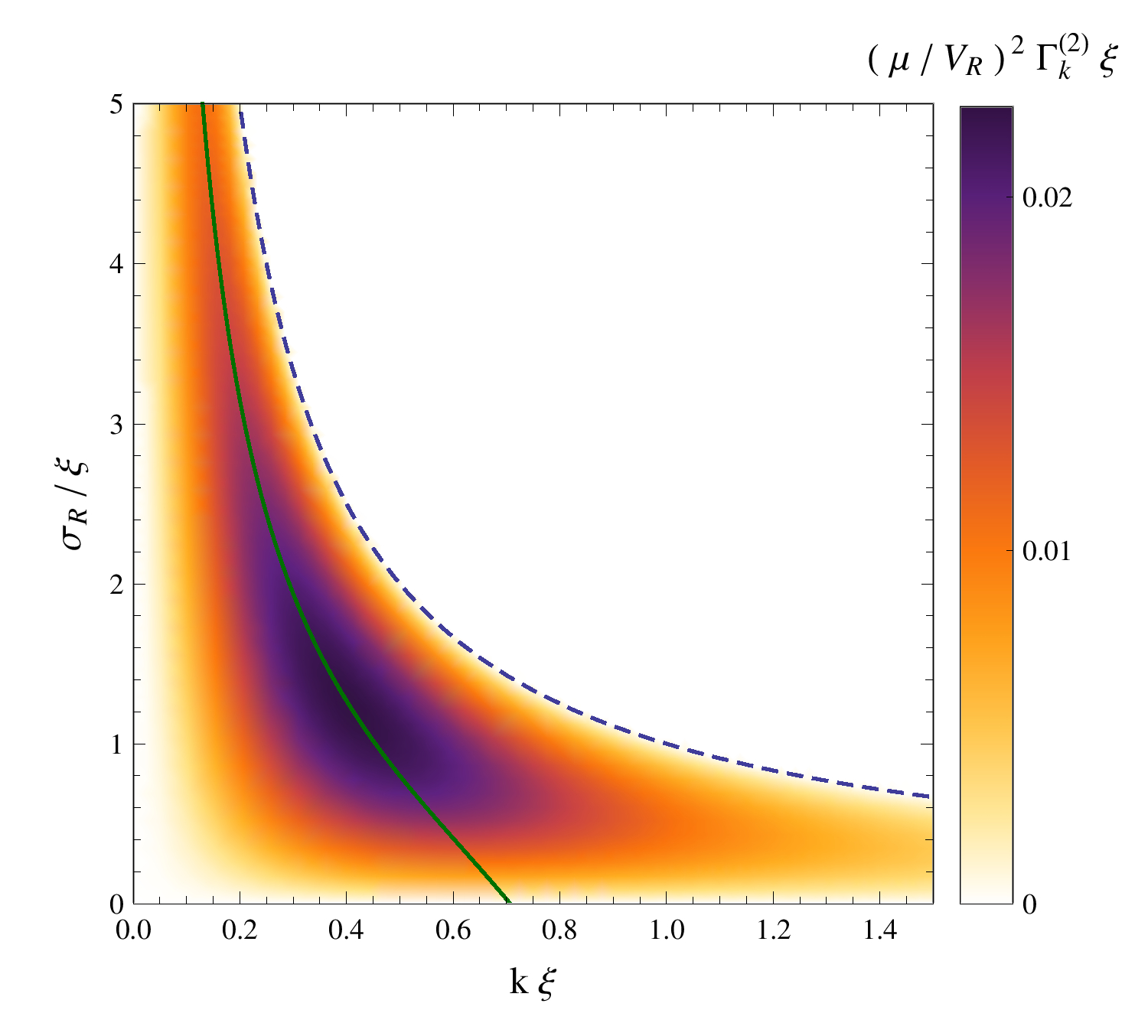
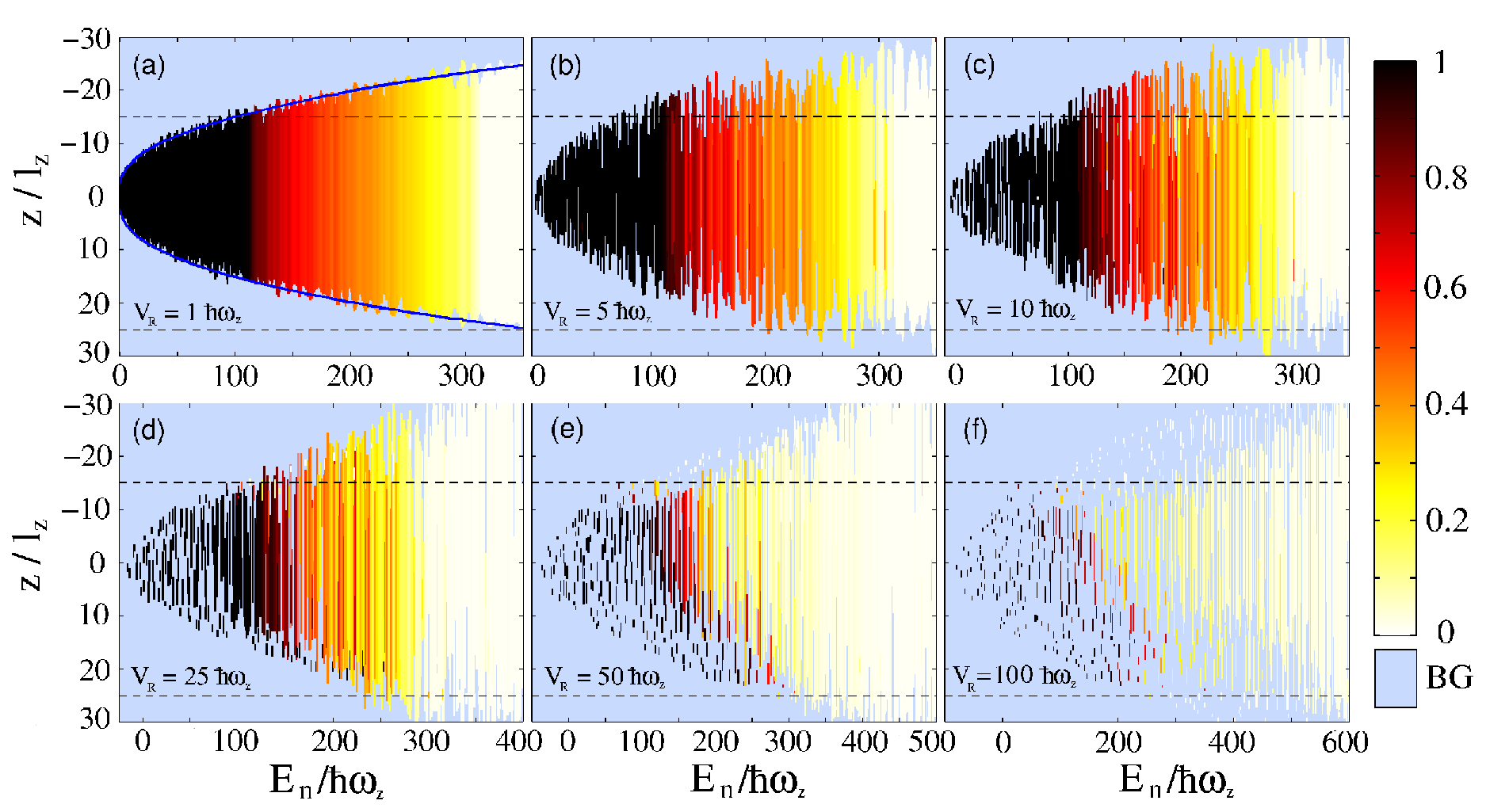
Abstract: We study the Anderson localization of Bogoliubov quasiparticles (elementary many-body excitations) in a weakly interacting Bose gas of chemical potential $mu$ subjected to a disordered potential V. We introduce a general mapping (valid for weak inhomogeneous potentials in any dimension) of the Bogoliubov-de Gennes equations onto a single-particle Schroedinger-like equation with an effective potential. For disordered potentials, the Schroedinger-like equation accounts for the scattering and localization properties of the Bogoliubov quasiparticles. We derive analytically the localization lengths for correlated disordered potentials in the one-dimensional geometry. Our approach relies on a perturbative expansion in $V/mu$, which we develop up to third order, and we discuss the impact of the various perturbation orders. Our predictions are shown to be in very good agreement with direct numerical calculations. We identify different localization regimes: For low energy, the effective disordered potential exhibits a strong screening by the quasicondensate density background, and localization is suppressed. For high-energy excitations, the effective disordered potential reduces to the bare disordered potential, and the localization properties of quasiparticles are the same as for free particles. The maximum of localization is found at intermediate energy when the quasicondensate healing length is of the order of the disorder correlation length. Possible extensions of our work to higher dimensions are also discussed.
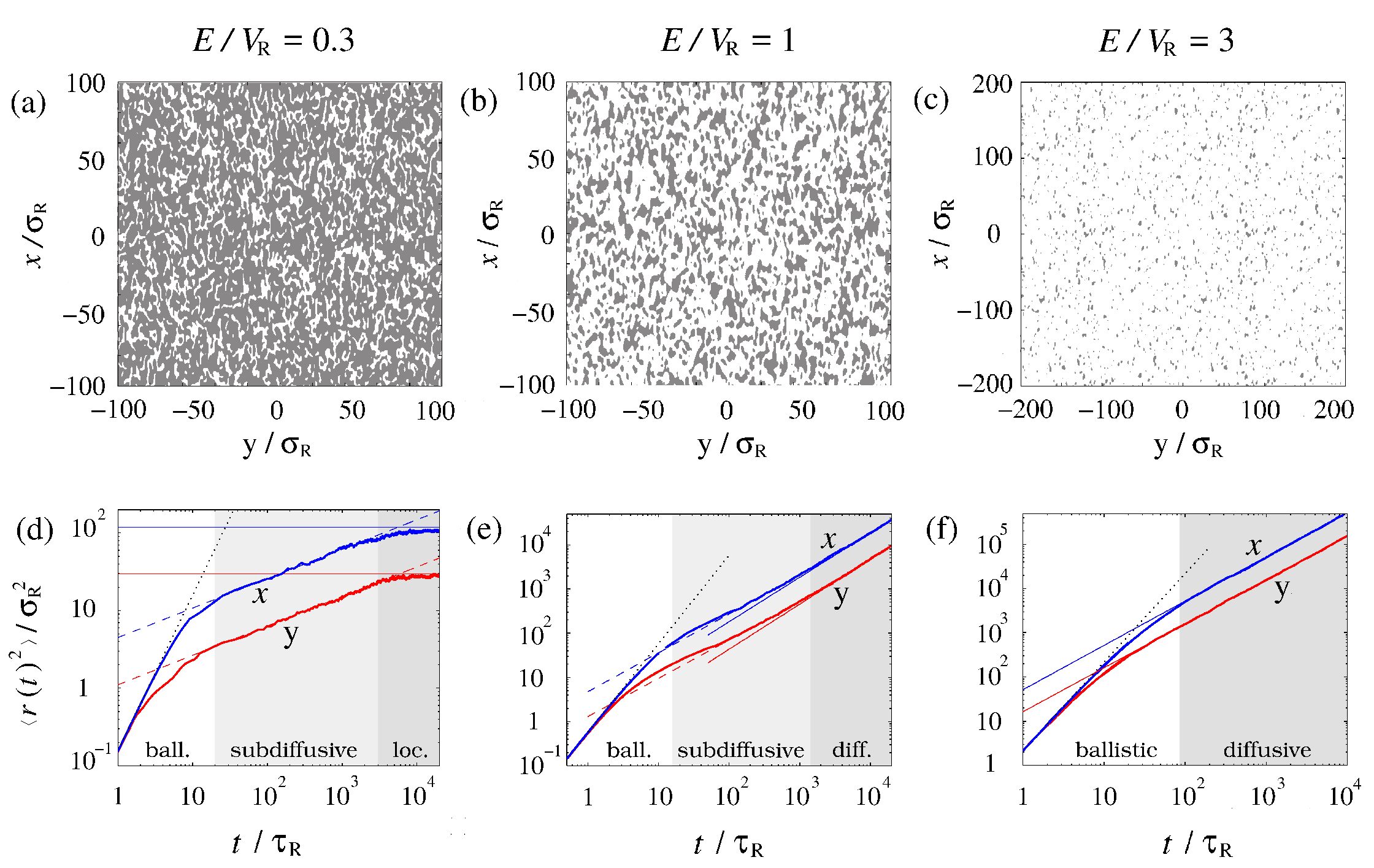
Abstract: We numerically study the dynamics of cold atoms in a two-dimensional disordered potential. We consider an anisotropic speckle potential and focus on the classical regime, which is relevant to some recent experiments. First, we study the behavior of particles with a fixed energy and identify different transport regimes. For low energy, the particles are classically localized due to the absence of a percolating cluster. For high energy, the particles undergo normal diffusion and we show that the diffusion constants scale algebraically with the particle energy, with an anisotropy factor which significantly differs from that of the disordered potential. For intermediate energy, we find a transient sub-diffusive regime, which is relevant to the time scale of typical experiments. Second, we study the behavior of a cold-atomic gas with an arbitrary energy distribution, using the above results as a groundwork. We show that the density profile of the atomic cloud in the diffusion regime is strongly peaked and, in particular, that it is not Gaussian. Its behavior at large distances allows us to extract the energy-dependent diffusion constants from experimental density distributions. For a thermal cloud released into the disordered potential, we show that our numerical predictions are in agreement with experimental findings. Not only does this work give insights to recent experimental results, but it may also serve interpretation of future experiments searching for deviation from classical diffusion and traces of Anderson localization.
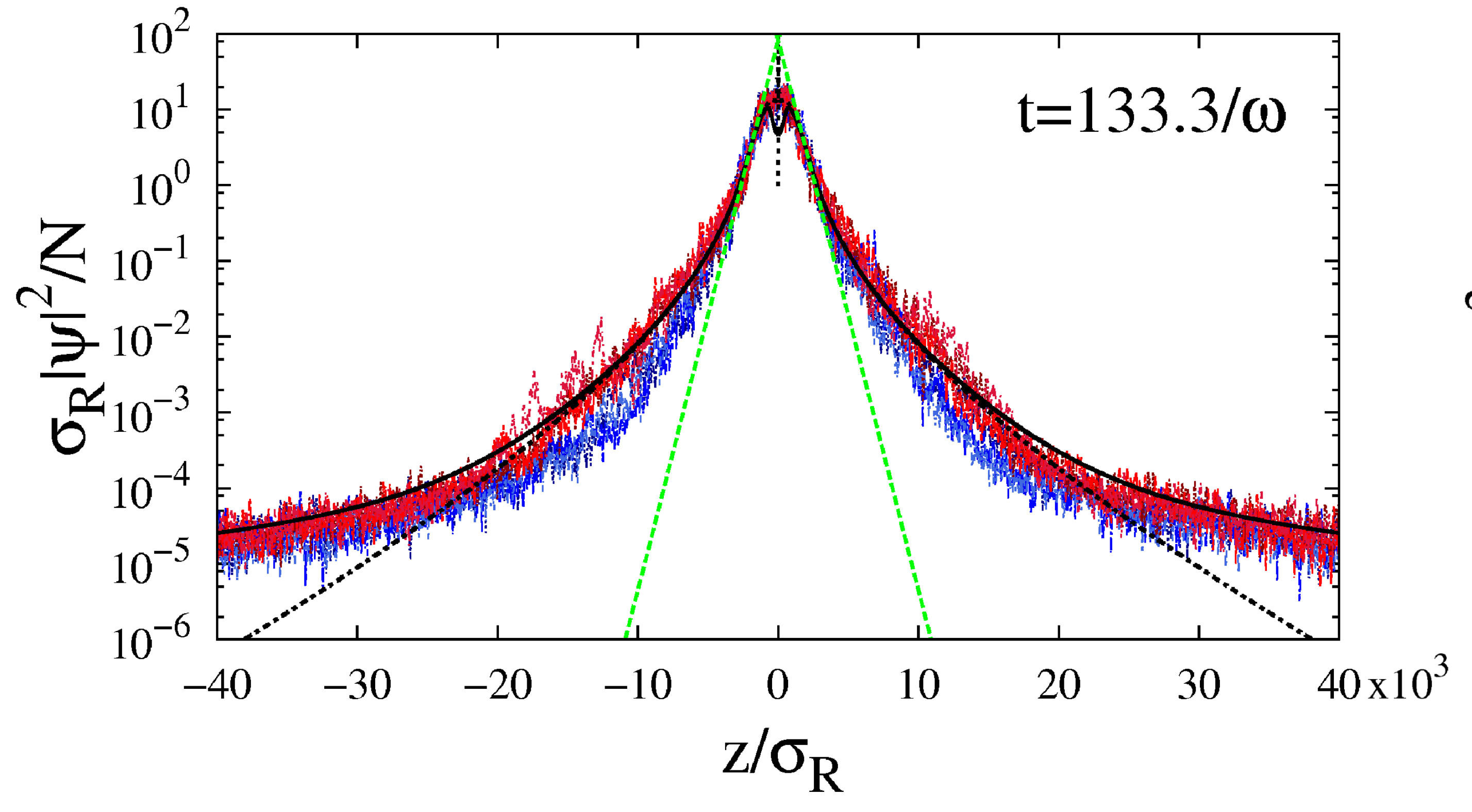
Abstract: We theoretically study the Anderson localization of a matter wave packet in a one-dimensional disordered potential. We develop an analytical model which includes the initial phase-space density of the matter wave and the spectral broadening induced by the disorder. Our approach predicts a behavior of the localized density profile significantly more complex than a simple exponential decay. These results are confirmed by large-scale and long-time numerical calculations. They shed new light on recent experiments with ultracold atoms and may impact their analysis.

Abstract: We study Anderson localization in a disordered potential combined with an inhomogeneous trap. We show that the spectrum displays both localized and extended states, which coexist at intermediate energies. In the region of coexistence, we find that the extended states result from confinement by the trap and are weakly affected by the disorder. Conversely, the localized states correspond to eigenstates of the disordered potential, which are only affected by the trap via an inhomogeneous energy shift. These results are relevant to disordered quantum gases and we propose a realistic scheme to observe the coexistence of localized and extended states in these systems.
Abstract: An experiment with ultracold gases reveals how weakly interacting atoms cooperate to protect long-range coherence against disorder-induced localization, and should offer insight into long-standing questions on the complex interplay of interactions and disorder in quantum systems.
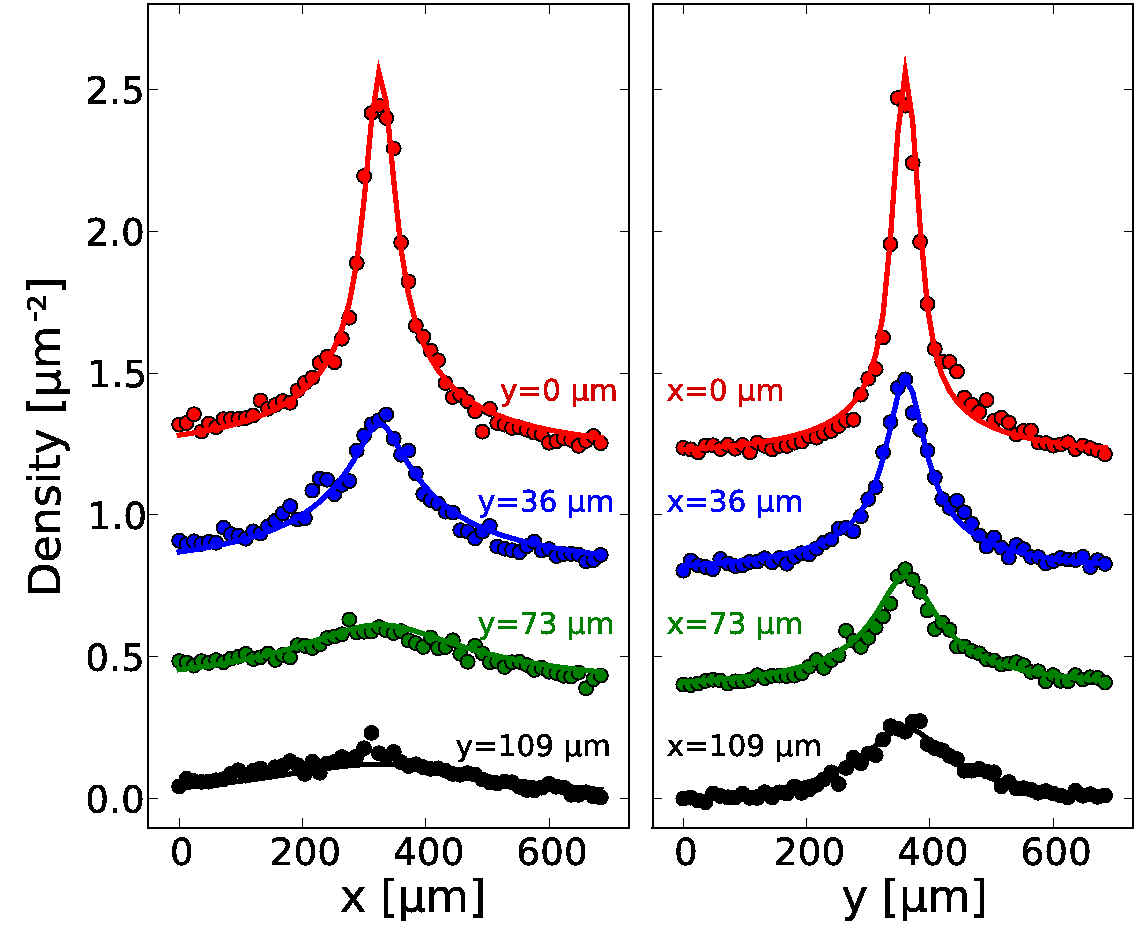
Abstract: We study the horizontal expansion of vertically confined ultra-cold atoms in the presence of disorder. Vertical confinement allows us to realize a situation with a few coupled harmonic oscillator quantum states. The disordered potential is created by an optical speckle at an angle of 30{deg} with respect to the horizontal plane, resulting in an effective anisotropy of the correlation lengths of a factor of 2 in that plane. We observe diffusion leading to non-Gaussian density profiles. Diffusion coefficients, extracted from the experimental results, show anisotropy and strong energy dependence, in agreement with numerical calculations.
Abstract: When attempting to understand the role of disorder in condensed-matter physics, we face considerable experimental and theoretical difficulties, and many questions are still open. Two of the most challenging ones-debated for decades-concern the effect of disorder on superconductivity and quantum magnetism. We review recent progress in the field of ultracold atomic gases, which should pave the way towards the realization of versatile quantum simulators, which help solve these questions. In addition, ultracold gases offer original practical and conceptual approaches, which open new perspectives to the field of disordered systems.
Abstract: We study Anderson localization of ultracold atoms in weak one-dimensional speckle potentials using perturbation theory beyond Born approximation. We show the existence of a series of sharp crossovers (effective mobility edges) between energy regions where localization lengths differ by orders of magnitude. We also point out that the correction to the Born term explicitly depends on the sign of the potential. Our results are in agreement with numerical calculations in a regime relevant for experiments. Finally, we analyze our findings in the light of a diagrammatic approach.
Abstract: We theoretically study the dipole oscillations of an ideal Fermi gas in a disordered trap. We show that even weak disorder induces strong damping of the oscillations and we identify a metal-insulator crossover. For very weak disorder, we show that damping results from a dephasing effect related to weak random perturbations of the energy spectrum. For increasing disorder, we show that the Fermi gas crosses over to an insulating regime characterized by strong damping due to the proliferation of localized states.
Abstract: In 1958, Anderson predicted the localization of electronic wavefunctions in disordered crystals and the resulting absence of diffusion. It is now recognized that Anderson localization is ubiquitous in wave physics because it originates from the interference between multiple scattering paths. Experimentally, localization has been reported for light waves, microwaves, sound waves and electron gases. However, there has been no direct observation of exponential spatial localization of matter waves of any type. Here we observe exponential localization of a Bose-Einstein condensate released into a one-dimensional waveguide in the presence of a controlled disorder created by laser speckle. We operate in a regime of pure Anderson localization, that is, with weak disorder-such that localization results from many quantum reflections of low amplitude-and an atomic density low enough to render interactions negligible. We directly image the atomic density profiles as a function of time, and find that weak disorder can stop the expansion and lead to the formation of a stationary, exponentially localized wavefunction-a direct signature of Anderson localization. We extract the localization length by fitting the exponential wings of the profiles, and compare it to theoretical calculations. The power spectrum of the one-dimensional speckle potentials has a high spatial frequency cutoff, causing exponential localization to occur only when the de Broglie wavelengths of the atoms in the expanding condensate are greater than an effective mobility edge corresponding to that cutoff. In the opposite case, we find that the density profiles decay algebraically. The method presented here can be extended to localization of atomic quantum gases in higher dimensions, and with controlled interactions.
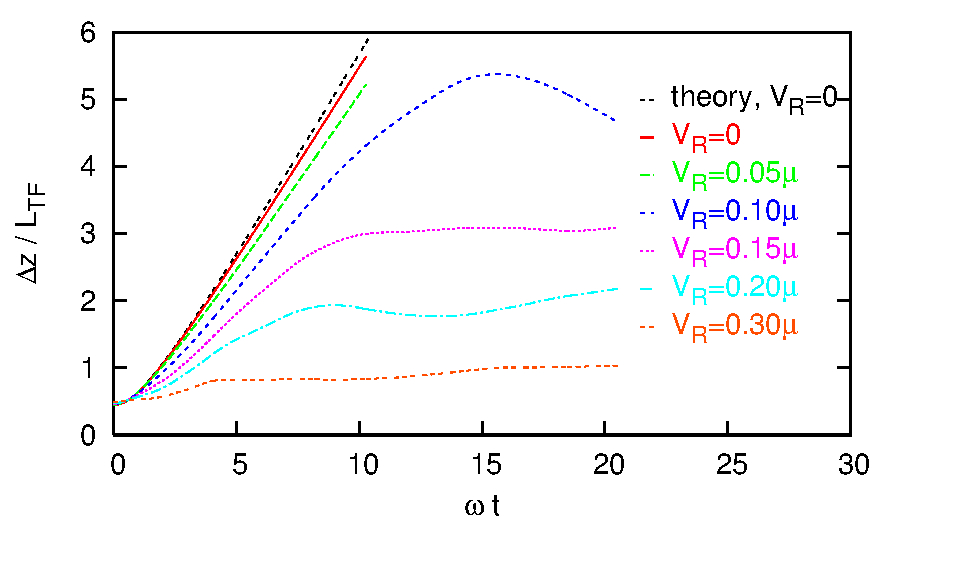
Abstract: We theoretically investigate the localization of an expanding Bose-Einstein condensate (BEC) with repulsive atom-atom interactions in a disordered potential. We focus on the regime where the initial inter-atomic interactions dominate over the kinetic energy and the disorder. At equilibrium in a trapping potential and for the considered small disorder, the condensate shows a Thomas-Fermi shape modified by the disorder. When the condensate is released from the trap, a strong suppression of the expansion is obtained in contrast to the situation in a periodic potential with similar characteristics. This effect crucially depends on both the momentum distribution of the expanding BEC and the strength of the disorder. For strong disorder, the suppression of the expansion results from the fragmentation of the core of the condensate and from classical reflections from large modulations of the disordered potential in the tails of the condensate. We identify the corresponding disorder-induced trapping scenario for which large atom-atom interactions and strong reflections from single modulations of the disordered potential play central roles. For weak disorder, the suppression of the expansion signals the onset of Anderson localization, which is due to multiple scattering from the modulations of the disordered potential. We compute analytically the localized density profile of the condensate and show that the localization crucially depends on the correlation function of the disorder. In particular, for speckle potentials the long-range correlations induce an effective mobility edge in 1D finite systems. Numerical calculations performed in the mean-field approximation support our analysis for both strong and weak disorder.
Abstract: We study a Brownian motor, based on cold atoms in optical lattices, where atomic motion can be induced in a controlled manner in an arbitrary direction, by rectification of isotropic random fluctuations. In contrast with ratchet mechanisms, our Brownian motor operates in a potential that is spatially and temporally symmetric, in apparent contradiction to the Curie principle. Simulations, based on the Fokker-Planck equation, allow us to gain knowledge on the qualitative behaviour of our Brownian motor. Studies of Brownian motors, and in particular ones with unique control properties, are of fundamental interest because of the role they play in protein motors and their potential applications in nanotechnology. In particular, our system opens the way to the study of quantum Brownian motors.
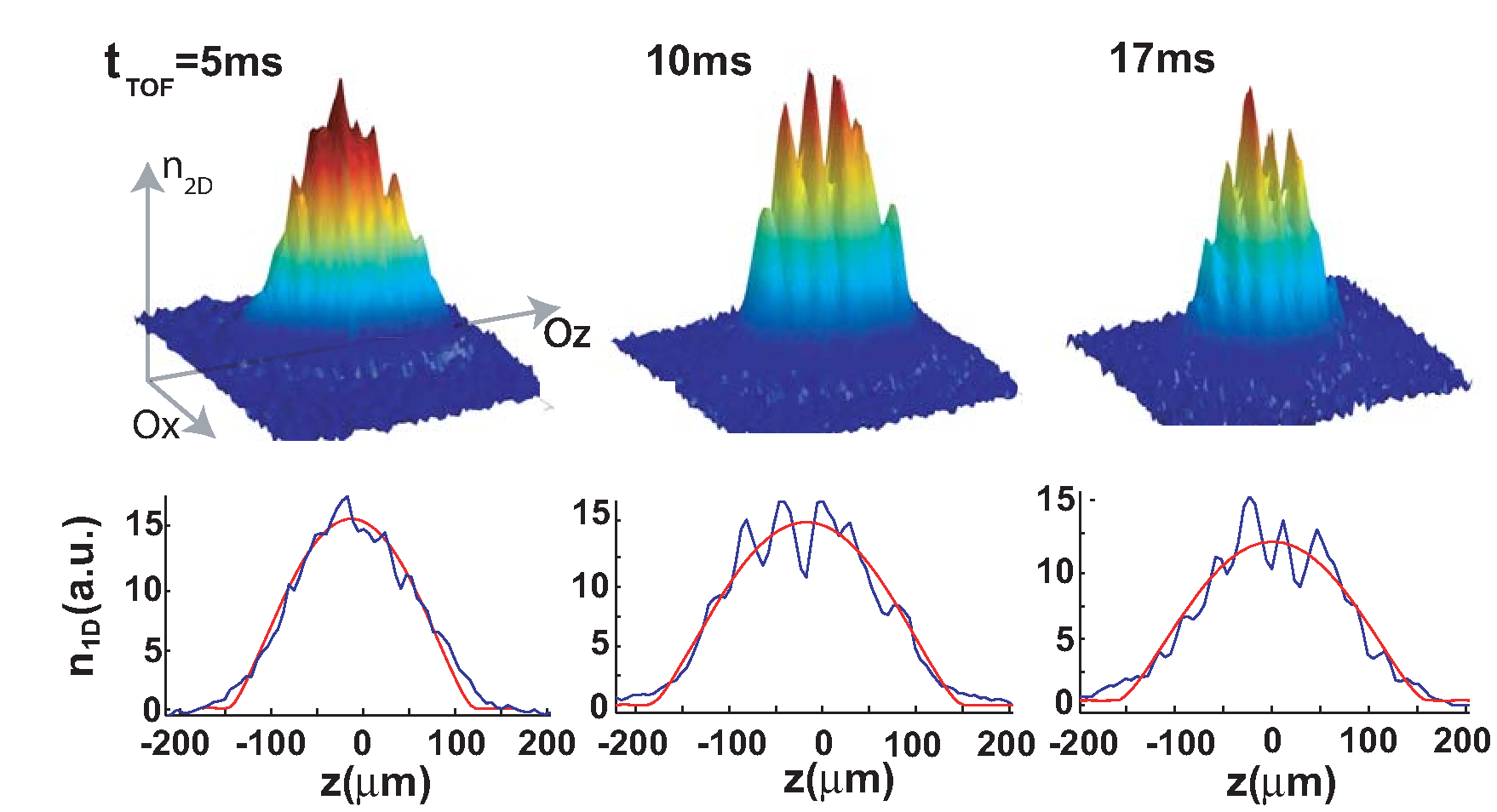
Abstract: We observe large density modulations in time-of-flight images of elongated Bose-Einstein condensates, initially confined in a harmonic trap and in the presence of weak disorder. The development of these modulations during the time of flight and their dependence with the disorder are investigated. We render an account of this effect using numerical and analytical calculations. We conclude that the observed large density modulations originate from the weak initial density modulations induced by the disorder and not from initial phase fluctuations (thermal or quantum).
Abstract: We propose and analyze a general mechanism of disorder-induced order in two-component Bose-Einstein condensates, analogous to corresponding effects established for XY spin models. We show that a random Raman coupling induces a relative phase of $pi/2$ between the two BECs and that the effect is robust. We demonstrate it in one, two, and three dimensions at T=0 and present evidence that it persists at small T>0. Applications to phase control in ultracold spinor condensates are discussed.
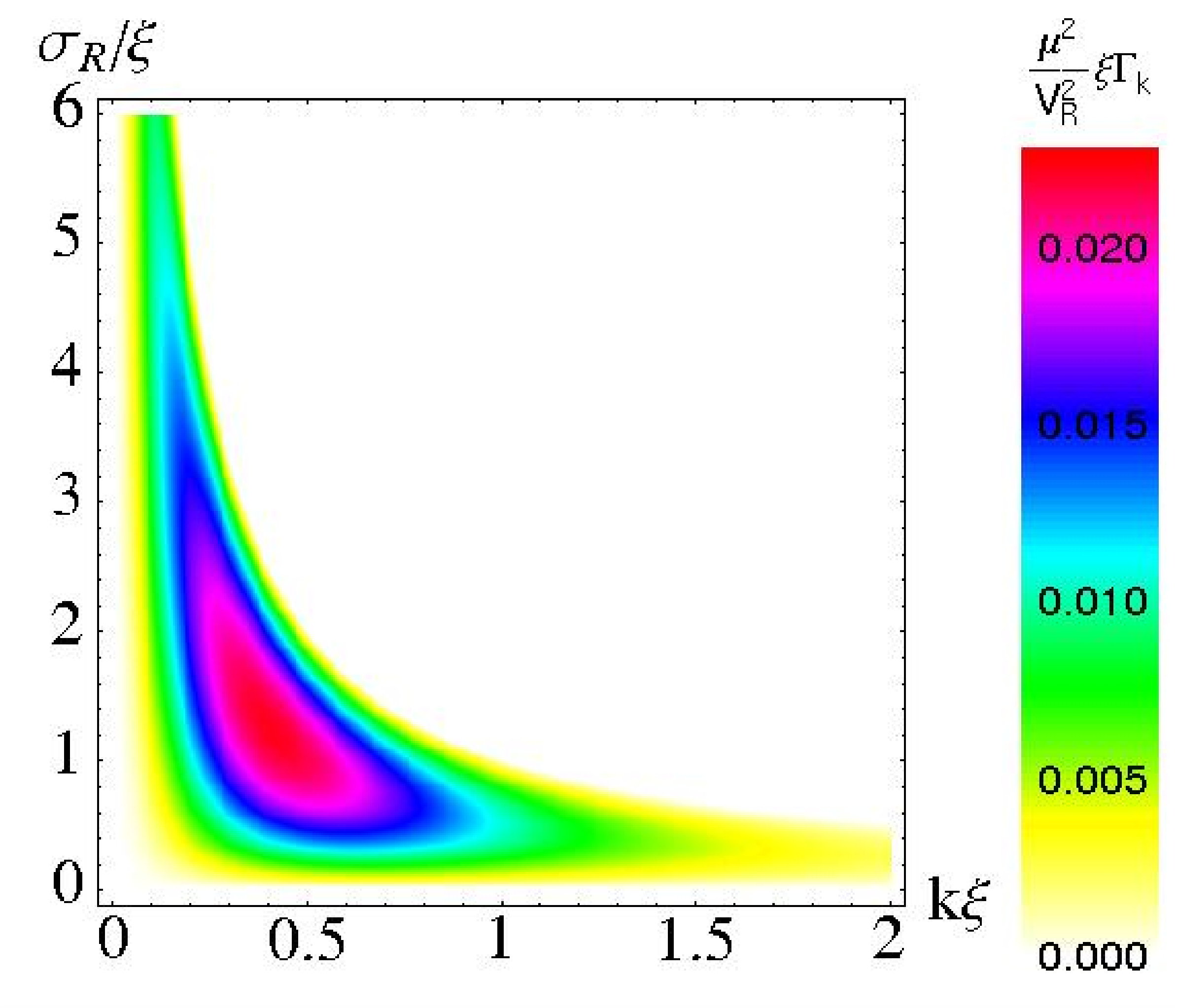
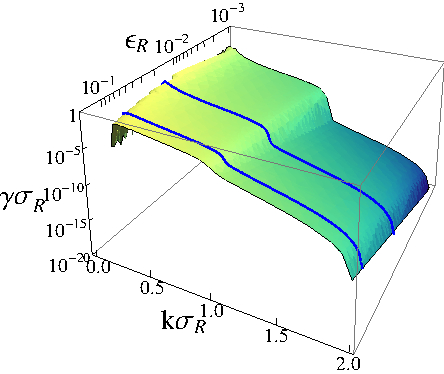
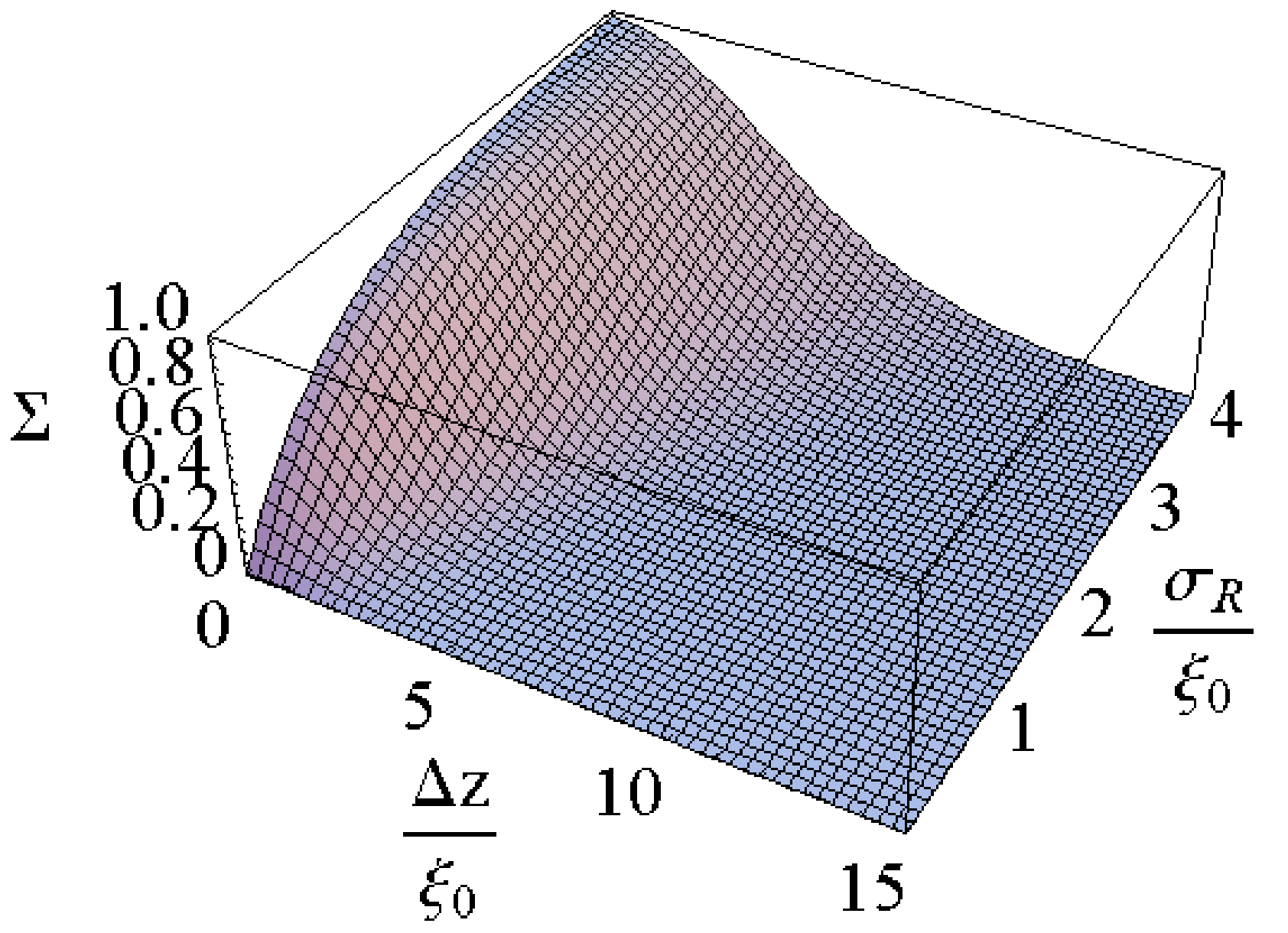
Abstract: We study the Anderson localization of Bogolyubov quasiparticles in an interacting Bose-Einstein condensate (with a healing length xi) subjected to a random potential (with a finite correlation length sigma_R). We derive analytically the Lyapunov exponent as a function of the quasiparticle momentum k, and we study the localization maximum k_{max}. For 1D speckle potentials, we find that k_{max} propto 1/xi when xi gg sigma_R while k_{max} propto 1/sigma_R when xi ll sigma_R, and that the localization is strongest when xi sim sigma_R. Numerical calculations support our analysis, and our estimates indicate that the localization of the Bogolyubov quasiparticles is accessible in experiments with ultracold atoms.
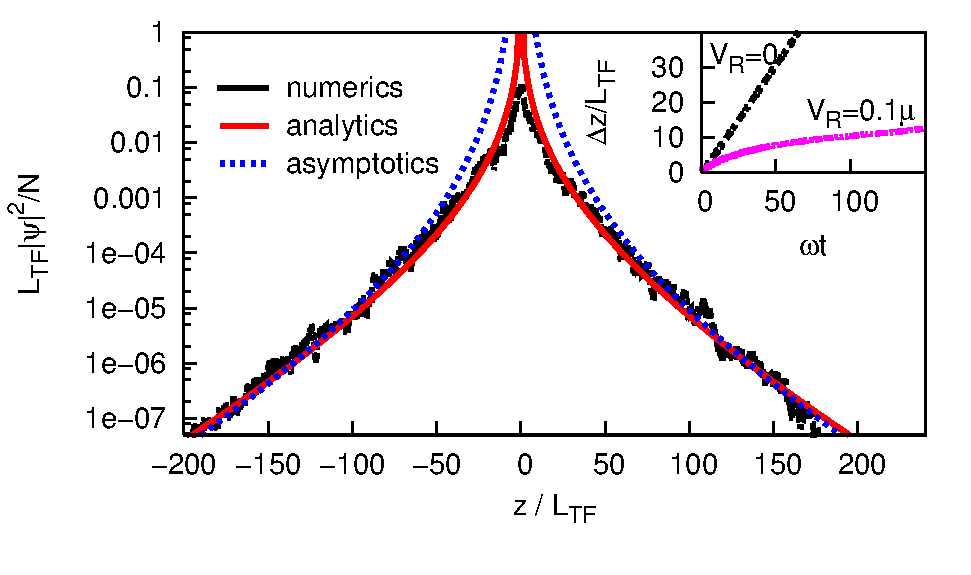
Abstract: We show that the expansion of an initially confined interacting 1D Bose-Einstein condensate can exhibit Anderson localization in a weak random potential with correlation length sigma_R. For speckle potentials the Fourier transform of the correlation function vanishes for momenta k>2/sigma_R so that the Lyapunov exponent vanishes in the Born approximation for k>1/sigma_R. Then, for the initial healing length of the condensate xi>sigma_R the localization is exponential, and for sigma_R>xi it changes to algebraic.
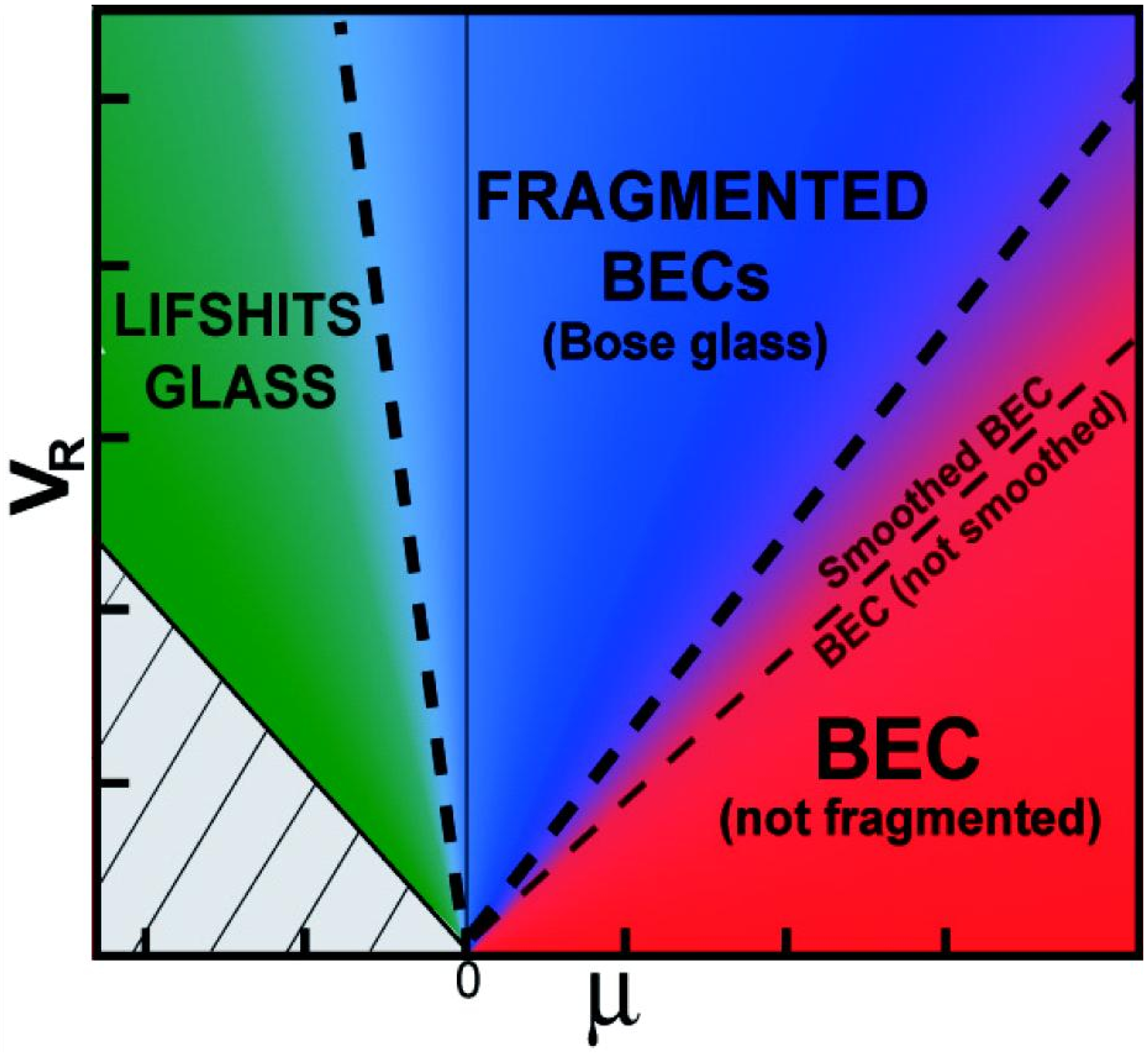
Abstract: We study an ultracold Bose gas in the presence of 1D disorder for repulsive interatomic interactions varying from zero to the Thomas-Fermi regime. We show that for weak interactions the Bose gas populates a finite number of localized single-particle Lifshits states, while for strong interactions a delocalized disordered Bose-Einstein condensate is formed. We discuss the schematic quantum-state diagram and derive the equations of state for various regimes.
Abstract: We theoretically investigate the physics of interacting Bose-Einstein condensates at equilibrium in a weak (possibly random) potential. We develop a perturbation approach to derive the condensate wave function for an amplitude of the potential smaller than the chemical potential of the condensate and for an arbitrary spatial variation scale of the potential. Applying this theory to disordered potentials, we find in particular that, if the healing length is smaller than the correlation length of the disorder, the condensate assumes a delocalized Thomas-Fermi profile. In the opposite situation where the correlation length is smaller than the healing length, we show that the random potential can be significantly smoothed and, in the mean-field regime, the condensate wave function can remain delocalized, even for very small correlation lengths of the disorder.
Abstract: We propose a general mechanism of random-field-induced order (RFIO), in which long-range order is induced by a random field that breaks the continuous symmetry of the model. We particularly focus on the case of the classical ferromagnetic XY model on a two-dimensional lattice, in a uniaxial random field. We prove rigorously that the system has spontaneous magnetization at temperature T=0, and we present strong evidence that this is also the case for small T>0. We discuss generalizations of this mechanism to various classical and quantum systems. In addition, we propose possible realizations of the RFIO mechanism, using ultracold atoms in an optical lattice. Our results shed new light on controversies in existing literature, and open a way to realize RFIO with ultracold atomic systems.
Abstract: Nous presentons une etude de l'expansion d'un condensat de Bose-Einstein dans un potentiel aleatoire 1D cree par une figure de tavelures. L'expansion du condensat et le mouvement de son centre de masse sont ralentis jusqu'a s'arreter en presence du potentiel aleatoire. Nous etudions ces deux effets en fonction de l'amplitude du potentiel dans une situation ou l'energie typique par particule est superieure a cette amplitude.
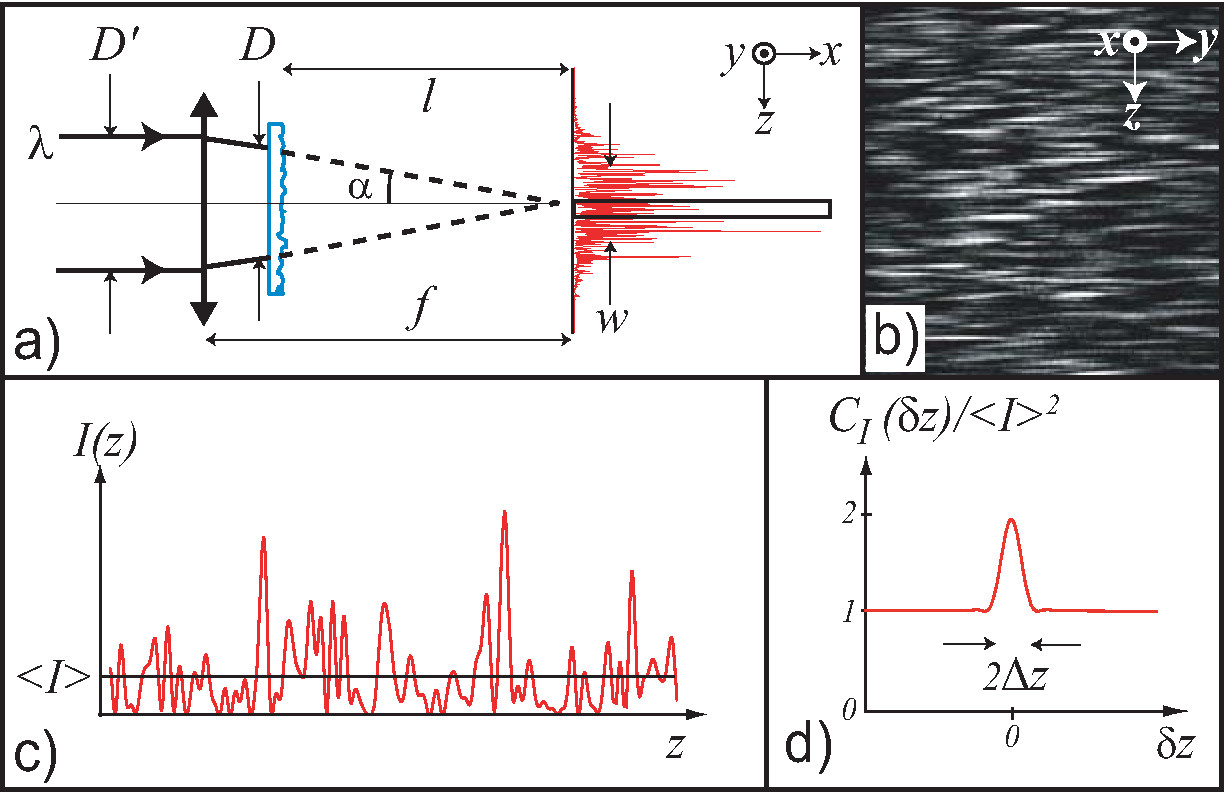
Abstract: We present a detailed analysis of the 1D expansion of a coherent interacting matterwave (a Bose-Einstein condensate (BEC)) in the presence of disorder. A 1D random potential is created via laser speckle patterns. It is carefully calibrated and the self-averaging properties of our experimental system are discussed. We observe the suppression of the transport of the BEC in the random potential. We discuss the scenario of disorder-induced trapping taking into account the radial extension in our experimental 3D BEC and we compare our experimental results with the theoretical predictions.
Abstract: We investigate theoretically the low-temperature physics of a two-component ultracold mixture of bosons and fermions in disordered optical lattices. We focus on the strongly correlated regime. We show that, under specific conditions, composite fermions, made of one fermion plus one bosonic hole, form. The composite picture is used to derive an effective Hamiltonian whose parameters can be controlled via the boson-boson and the boson-fermion interactions, the tunnelling terms and the inhomogeneities. We finally investigate the quantum phase diagram of the composite fermions and show that it corresponds to the formation of Fermi glasses, spin glasses and quantum percolation regimes.
Abstract: Cold atomic gases placed in optical lattices enable studies of simple condensed matter theory models with parameters that may be tuned relatively easily. When the optical potential is randomized (e.g. using laser speckle to create a random intensity distribution) one may be able to observe Anderson localization of matter waves for non-interacting bosons, the so-called Bose glass in the presence of interactions, as well as the Fermi glass or quantum spin glass for mixtures of fermions and bosons.
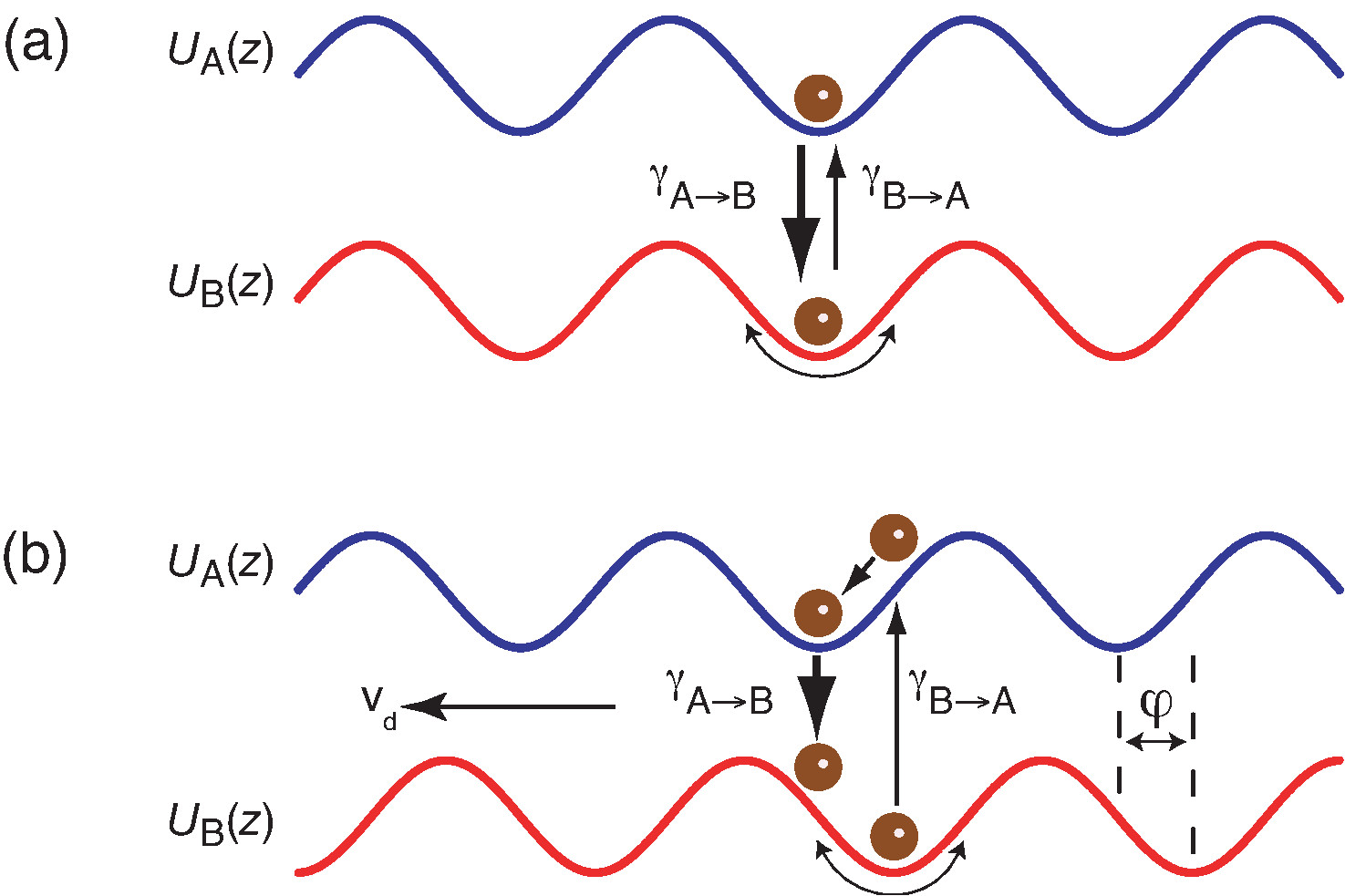
Abstract: We demonstrate a Brownian motor, based on cold atoms in optical lattices, where isotropic random fluctuations are rectified in order to induce controlled atomic motion in arbitrary directions. In contrast to earlier demonstrations of ratchet effects, our Brownian motor operates in potentials that are spatially and temporally symmetric, but where spatiotemporal symmetry is broken by a phase shift between the potentials and asymmetric transfer rates between them. The Brownian motor is demonstrated in three dimensions and the noise-induced drift is controllable in our system.